Horizonte de Estudo¶
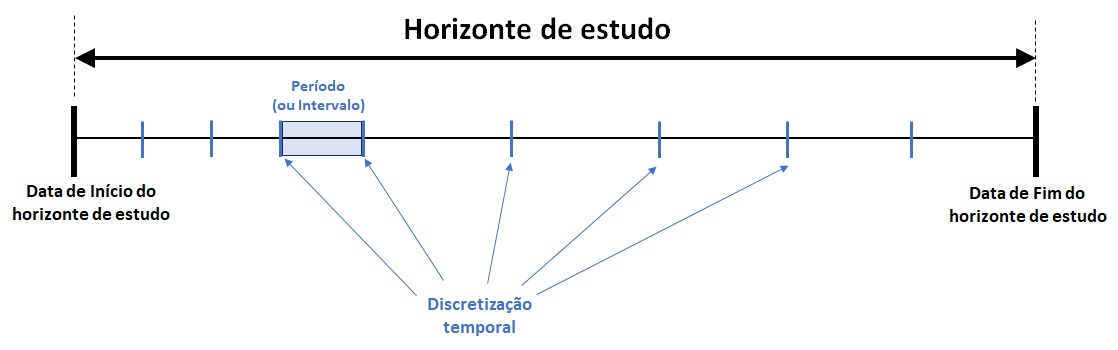
O horizonte de estudo corresponde ao intervalo de tempo compreendido entre a desde a data do instante inicial até a data do instante final do estudo, ou seja, é a duração total do período de estudo.
Este horizonte é função do nível de planejamento a ser realizado: estratégico (de mais longo prazo), tático (médio prazo) ou operacional (curto prazo).
Neste manual, o número de períodos no horizonte de estudo é denotado por \(T\), e a duração de cada período t é denotado por \({\Delta}_t\).
Discretização Temporal¶
A discretização temporal corresponde ao grau de refinamento (intervalos de tempo) para os quais estarão associadas as decisões a serem determinadas pelo modelos. A partir da discretização temporal é que são definidos os Períodos de tempo do estudo.
Em geral, modelos de planejamento a mais longo prazo tendem a ter uma discretização temporal mais grossa, ou seja, os períodos possuem maior duração (ex: semanas ou meses), enquanto os modelos de mais curto prazo possuem períodos de tempo de menor duração (ex: meia hora ou horário).
No entanto, o aumento no grau de penetração nas fontes intermitentes de energia tem motivado à análise de granularidades de tempo mais finas mesmo em estudos de médio/longo prazos, o que é possível com a Integração direta entre modelos de longo e curtíssimo prazos.
Períodos de tempo¶
O período de tempo corresponde a cada intervalo na discretização temporal do estudo, para o qual estão associadas algumas variáveis de de decisão e restrições físicas e operativas para os componentes dos sistemas elétricos. Este termo também é comumente chamado de “estágio”, uma vez que, nos modelos que aplicam decomposição temporal para resolução do problema, como o NEWAVE e o DECOMP (modo Benders), cada estágio em que o problema é decomposto corresponde, em geral, a um período de tempo.
Neste manual, o índice de cada período \(T\), e a duração de cada período por \({\Delta}_T\).
Ressalta-se que podem ser considerados também diferentes cenários ao longo do horizonte de estudo (para os modelos NEWAVE e DECOMP), assim como representar Patamares de Carga não cronológicos dentro de cada período, para refinar as decisões dentro de cada período, quando estes compreendem intervalos de tempo maiores (ex: semanal, mensal) como nos modelos NEWAVE e DECOMP.
Patamares de Carga¶
A consideração de intervalos de tempo de duração mensal não permite representar de forma direta as variações de alguns dados de entrada ao longo do mês, principalmente os dados de carga, que apresentam uma sazonalidade marcante ao longo do dia e também durante as semanas. Como a energia não pode ser estocada em grandes volumes, a representação dos dados e restrições apenas a partir de seus valores médios poderia resultar em uma perda grande de precisão na representação do problema, principalmente em relação aos requisitos de potência, pois não seria possível representar os picos de carga.
Por outro lado, ainda que se fizesse um refinamento de forma pura e simples da discretização temporal para a consideração de períodos semanais ou até diários, ainda assim não se conseguiria tratar adequadamente estas variações diárias, e levaria a um aumento excessivo no esforço computacional para resolver o problema.
Desta forma, para que seja possível representar os picos de carga e outros dados e restrições que impõem o atendimento a condições associadas à potência em subintervalos de um estágio, os modelos de otimização energética do CEPEL que utilizam uma maior granularidade temporal (MELP, NEWAVE, DECOMP) permitem a subdivisão de cada período em patamares de carga.
cujo principal objetivo é representar a variação, ao longo do mês, de alguns dados de entrada do problema
A figura ilustra a definição desses patamares, a partir dos dados de carga horários.
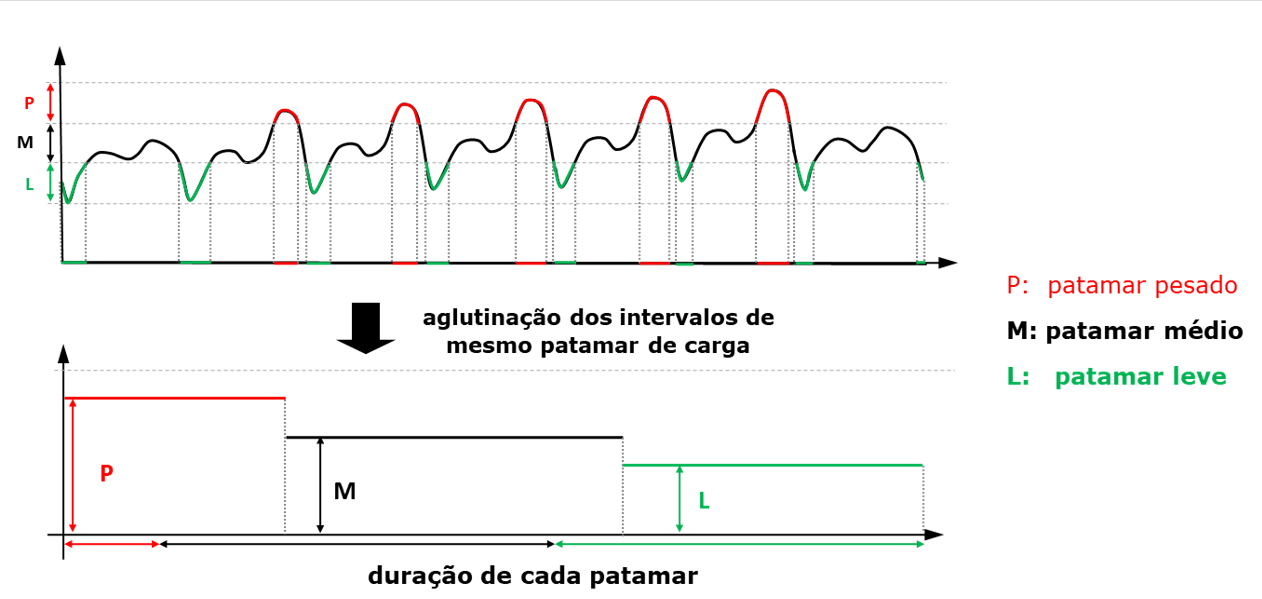
Ressalta-se que estes patamares são não cronológicos, ou seja, não há uma dependência temporal entre eles, e a única condição que deve ser respeitada é que a soma das durações de cada patamar em determinado estágio deve corresponder à duração total do estágio.
A definição dos patamares de carga é um dado de entrada dos modelos, e a ferramenta utilizada no sistema brasileiro para sua definição nos processos de Programa Mensal da Operação (PMO) e planejamento é o programa MODCAR, desenvolvido pelo CEPEL. 1
Horário de Verão¶
Nos sistemas em que existe horário de verão, este aspecto, apesar de aparentemente ser um detalhe da operação do sistema, torna-se importante em um modelo de discretização horária como o DESSEM. Uma vez informado ao modelo a entrada ou saída do horário de verão para determinado dia do horizonte de estudo do DESSEM, o modelo automaticamente tratará a leitura dos dados de entrada e a resolução do problema considerando uma hora a menos ou a mais para esse dia, respectivamente. Detalhes devem ser consultados no Manual do Usuário do modelo.
Em virtude da não utilização do horário de verão no Brasil atualmente, as execuções oficiais dos modelos não têm utilizado essa funcionalidade.
Ano Bissexto¶
A identificação de ano bissexto é feita automaticamente pelos modelos DECOMP e DESSEM, em função da data de início do estudo informada pelo usuário, considerando desta forma o mês de fevereiro com 29 ou 28 dias, dependendo do caso. Não é necessário nenhum dado ou tratamento do usuário em relação a esse aspecto.
Ressalta-se que, como no modelo NEWAVE a representação temporal é feita considerando todos os meses com a mesma duração média, não se aplica a particularidade referente a ano bissexto nesse modelo.
Taxa de Desconto¶
Durante as etapas de cálculo da política de operação, despacho e eventuais simulações com os modelos, deve-se calcular o valor esperado do custo de operação do sistema e o custo marginal de operação para cada submercado. Desta forma, torna-se necessário trazer a valor presente os custos que não foram calculados no início do horizonte de estudo, utilizando uma taxa de desconto que, aplicada a um custo futuro, determinará sua equivalência no presente.
A taxa de desconto \(beta\) é fornecida através de um valor anual (ex: 12%a.a), a partir do qual pode se calcular o valor \(C_p\), avaliado em um instante presente \(t\), de determinado custo \(C\) incorrido a \(k\) meses no futuro (ou seja, no período \(t+k\), através da seguinte expressão:
\(C_p = \frac{C}{{(1+\frac{\beta}{100})}^k}\)
Configuração Dinâmica¶
Os modelos podem considerar uma configuração dinâmica, ou seja, a topologia e os dados de cadastro podem ser modificados ao longo do período de estudo. Com isso, podem ser definidas usinas e/ou máquinas hidroelétricas e térmicas que só começam a operar ao longo do horizonte de estudo, representando-se de forma adequada a expansão do sistema ao longo do horizonte de estudo.
Representação Temporal em cada Modelo¶
Descreve-se a seguir, em linhas gerais, como esses dois aspectos são definidos em cada modelo.
Modelo NEWAVE¶
Horizonte de Planejamento¶
O horizonte de planejamento do modelo NEWAVE (também denominado período de planejamento) é de 5 a 15 anos, e corresponde ao período de estudo propriamente dito, para o qual podem ser avaliados os resultados de desempenho do sistema obtidos pelo modelo. Além desse horizonte, o modelo NEWAVE pode considerar também:
Período pré, com duração de até 5 anos, que possui configuração estática e cujo principal objetivo é fazer com que o modelo perca a influência de suas condições iniciais (armazenamento e afluências passadas). Este período é indicado quando se deseja avaliar o desempenho do sistema não condicionado ao estado inicial;
Período pós, com duração de até 5 anos, cujo principal objetivo é fazer com que o modelo perca o efeito de “fim do mundo”, ou seja, evitar que o uso de uma função de custo futuro nula no final do horizonte afete os resultados ao longo do período de planejamento.
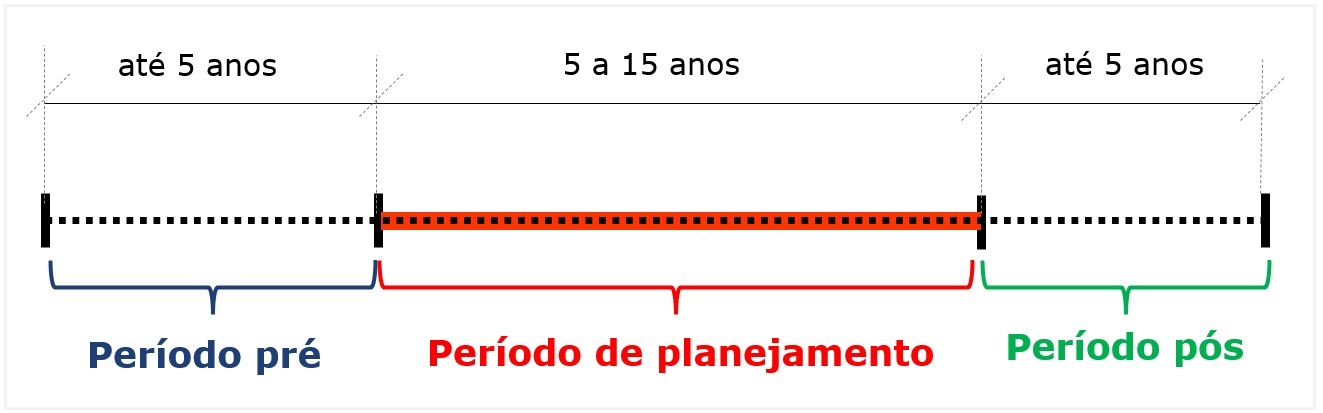
As configurações usuais dos períodos de planejamento, pré e pós do NEWAVE nas aplicações oficiais do modelo são:
casos de Programa Mensal da Operação (PMO): período de planejamento de 5 anos, sem período pré e período pós de 5 anos;
casos de Plano Decenal da Expansão (PDE): período de planejamento de 10 anos, sem período pré e período pós de 5 anos;
casos de Garantia Física (GF): período de planejamento de 15 anos, períodos pré e pós de 5 anos
Instante de fim do Horizonte de estudo¶
O modelo NEWAVE assume sempre que o final do horizonte será no final do último ano de estudo (Dezembro). Portanto, no esquema de horizonte rolante que é aplicado nos processos de PMO/PLD, a duração do horizonte de planejamento varia entre 109 meses (PMO de Dezembro) e 120 meses (PMO de Janeiro).
Acoplamento com a Função de custo futuro do período pós¶
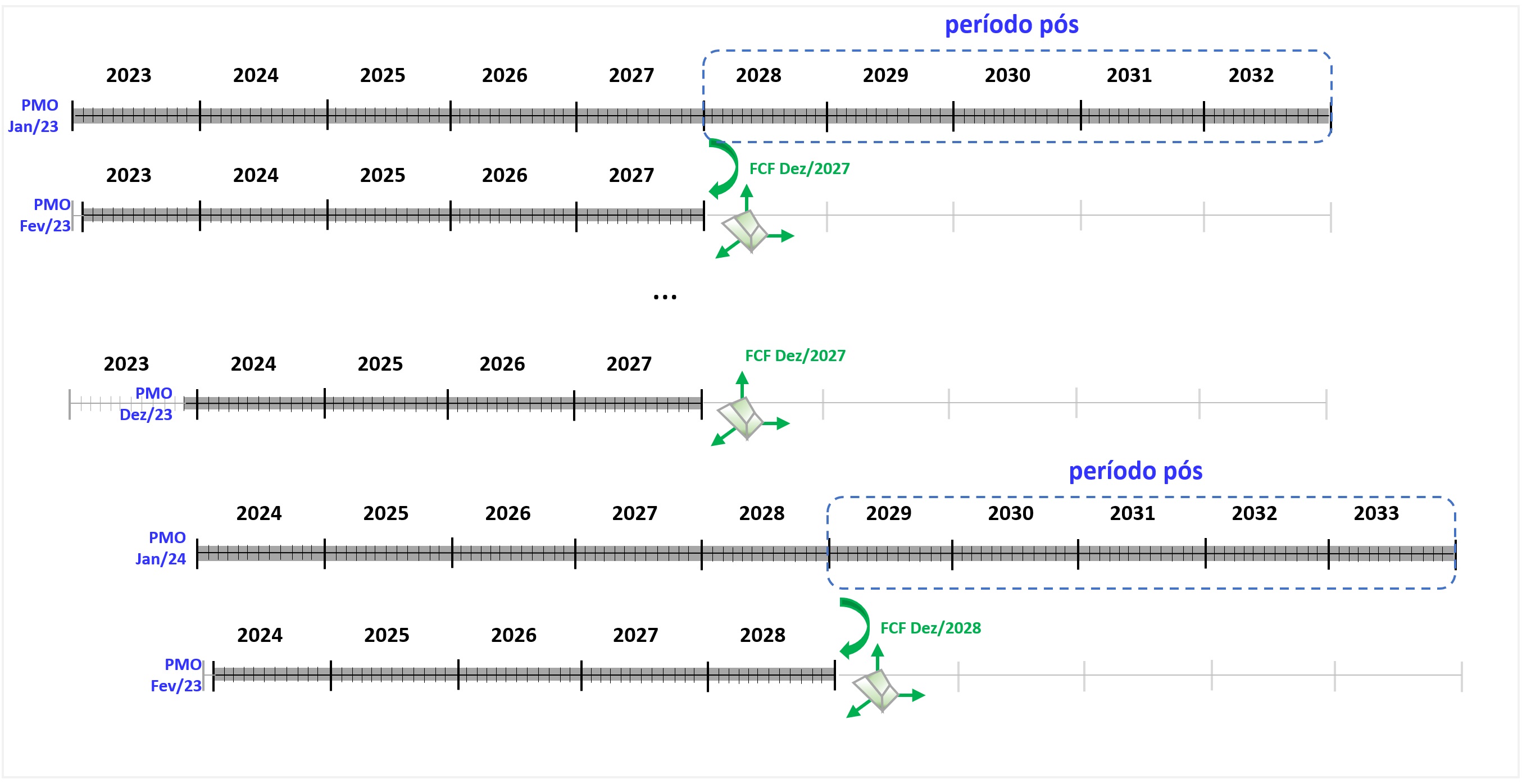
A partir de dezembro/2022 o NEWAVE passou a ter a opção de acoplar, ao final do horizonte de planejamento, com uma função de custo futuro fornecida externamente. Esta função tem o objetivo de ser uma condição de contorno para o final do horizonte de planejamento, valorando a água nos reservatórios e eliminando, portanto, a necessidade de inclusão de um horizonte pós para evitar o efeito de “fim de mundo” . Esta função, que é calculada em uma execução prévia do NEWAVE contendo o período pós estudo, deve ser atualizada periodicamente, como ilustrado a seguir, onde se sugere uma atualização anual.
A principal motivação para utilização dessa FCF ao final do horizonte de planejamento é a redução do tempo computacional para resolução do problema visto que:
a quantidade de subproblemas a serem resolvidos é menor e, portanto, cada iteração da PDDE levará menos tempo para ser processada;
a primeira iteração do NEWAVE já partirá com uma boa aproximação para a FCF ao final do horizonte de planejamento . Portanto, espera-se que a quantidade de iterações necessárias para se atingir o mesmo nível de convergência para a PDDE seja inferior em relação ao caso em que não se utilizou a FCF ao final do horizonte.
Algumas considerações e ressalvas, mencionadas a seguir, são importantes para a utilização dessa FCF ao final do horizonte do modelo NEWAVE.
Consistência estrutural¶
Para que haja o correto acoplamento da FCF com o subproblema em que os cortes serão inseridos (ou seja, o subproblema associado ao último período do horizonte de planejamento), é importante que as informações e estrutura da FCF no caso em que foi construída seja compatível com a estrutura das funções de custo futuro do caso em que é utilizada, ou seja:
o mês/ano referente à FCF do caso de origem (onde a FCF foi construída) deve ser o mesmo associado ao final de horizonte do caso em que é utilizada;
os conjuntos de variáveis de estado dos dois casos para o mês de acoplamento devem ser compatíveis, ou seja:
a quantidade de REEs ou o número de usinas hidrelétricas deve ser igual ao do caso em que está sendo utilizada a FCF, conforme o tipo de representação da configuração hidrelétrica (a reservatórios equivalentes ou usinas individualizadas);
a quantidade de submercados com usinas GNL, os lags máximos de antecipação de despacho e o número e duração dos patamares (vide seção 16.4) devem ser os mesmos;
a ordem máxima dos modelos autorregressivos (PAR(p)) entre os dois casos deve ser a mesma;;
as opções de uso de PAR(p)-A, uso da SAR, uso de VMINOP devem ser as mesmas nos dois casos.
Hipóteses para utilização da FCF ao final do horizonte de planejamento¶
A utilização de uma FCF pós parte da hipótese fundamental de que, ao resolver os problemas do NEWAVE no início de cada mês ao longo do ano (de acordo com a estratégia de Execução Encadeada dos Modelos, segundo um horizonte rolante), as alterações de dados dos subproblemas a serem resolvidos no período são mínimas.
Nesta situação, tomando como exemplo o esquema apresentado anteriormente, pode-se considerar que a FCF que foi calculada durante a estratégia de PDDE para o último mês do horizonte de planejamento (Dez/2027) na execução do NEWAVE no PMO de Jan/2023 é praticamente a mesma que seria calculada ao executar o NEWAVE no PMO de Fev/2023.
Cabe ressaltar que, na inexistência de qualquer alteração de dados de 2028 em diante entre os casos do PMOs de Jan e Fev/2023, a FCF teórica (ou seja, completa e exata) no final de Dez/2027 é exatamente a mesma para os dois casos, pois esta depende apenas dos dados futuros (após 2027), e não dos dados anteriores a Jan/2028.
Observa-se também que, na prática os cenários (aberturas) backward que foram gerados para o período pós do caso de origem da FCF seriam possivelmente diferentes daqueles que seriam gerados caso fosse adotado um período pós no caso de destino (que usa a FCF). Isso faria com que, em tese, as FCF teóricas ao final do período de planejamento fossem diferente entre os dois casos. Entretanto, como a diferença entre as afluências no período pós estaria associada somente à aleatoriedade inerente da utilização de ruídos para a geração de cenários, considera-se que esses cenários são estatisticamente equivalentes para a precisão adotada, e que está associada à quantidade de cenários backward. Por consequência, as FCFs ao final do horizonte de planejamento dos dois casos também seriam equivalentes, o que justificaria o uso dessa funcionalidade.
Aspectos associados à estratégia de solução por PDDE¶
Alguns aspectos relacionados à aplicação da estratégia de PDDE devem ser observados quando da utilização da FCF no final do horizonte de planejamento:
os estados que foram visitados ao final do horizonte de planejamento no caso de origem (construção da FCF) serão, na prática, diferentes dos estados visitados neste mesmo instante de tempo para o caso no qual a função foi utilizada. Ou seja, os cortes da FCF do final do horizonte de planejamento (que corresponde ao custo de operação no período pós no caso de origem) não foram construídos nos mesmos estados que foram visitados ao se executar o caso de destino. Entretanto, dada a distância temporal existente entre os instantes de início e final do horizonte de planejamento, considera-se que esses estados são estatisticamente equivalentes;
no cálculo do limite superior (ZSUP) para convergência da PDDE , considera-se, em cada série, a soma dos custos presentes de todos os estágios. No caso da aplicação de uma FCF ao final do horizonte, deve-se considerar também o custo futuro deste último estágio no cálculo do ZSUP, visto que este custo futuro não deve ser visto como um “corte de Benders” para a resolução do problema por PDDE, mas sim como uma condição de contorno que foi estabelecida ao final do horizonte de planejamento, e que faz parte, por tanto, da estrutura do subproblema do último estágio.
Discretizacao Temporal¶
A discretização temporal utilizada atualmente no modelo NEWAVE é mensal ao longo de todo o horizonte de estudo, sendo cada período podendo ser dividido em vários Patamares de Carga.
Observam-se ainda os seguintes aspectos na discretização temporal utilizado no modelo:
Duração dos meses civis¶
Não se faz distinção entre os meses de estudo em termos de duração. Portanto, todos os meses são considerados com uma duração média de 730 horas. Apesar de esta hipótese apresentar certo descolamento com a duração real dos meses, facilita a comparação entre a operação dos diferentes meses em relação aos resultados de energia, que seriam impactados com a duração de cada período.
Horário de Verão¶
Em virtude de sua discretização temporal menos refinada, o efeito da eventual adoção de horário de verão não é considerado no modelo NEWAVE.
Modelo DECOMP¶
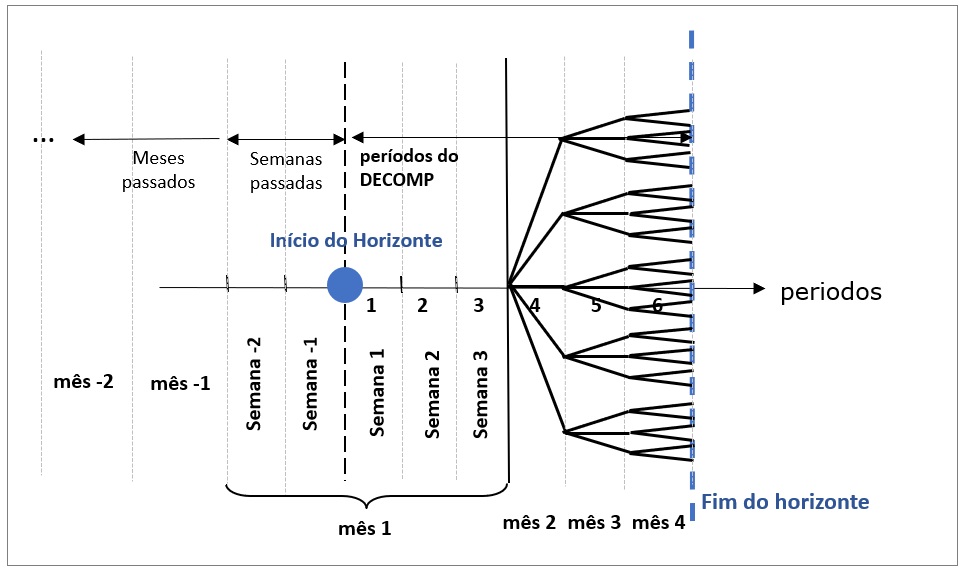
O horizonte de estudo do modelo DECOMP é de até 2 anos, sendo possível utilizar a discretização semanal para o primeiro mês de estudo e discretização mensal para os demais meses do horizonte.
A figura a seguir ilustra esse esquema típico, indicando o primeiro mês determinístico discretizado em semanas, e os meses seguintes estocásticos acoplando ao final com a função de custo futuro.
Modelo DESSEM¶
O horizonte de estudo no modelo DESSEM é de até 14 dias, com possibilidades de discretização em intervalos de meia-hora, 1 hora ou em patamares cronológicos de duração variável.
A figura a seguir ilustra esse esquema típico, indicando, à direita, o acoplamento entre os modelos DECOMP e DESSEM, que é importante para que o DECOMP transmita, ao modelo DESSEM, os valores da água nos reservatórios ao final de sua semana operativa. Adicionalmente, o acoplamento entre os resultados dos modelos pode ser reforçado estabelecendo metas semanais de geração térmica ou metas semanais de intercâmbio entre os submercados para o horizonte de estudo do DESSEM, além de metas de armazenamentos mínimos ou máximos finais nos reservatórios.
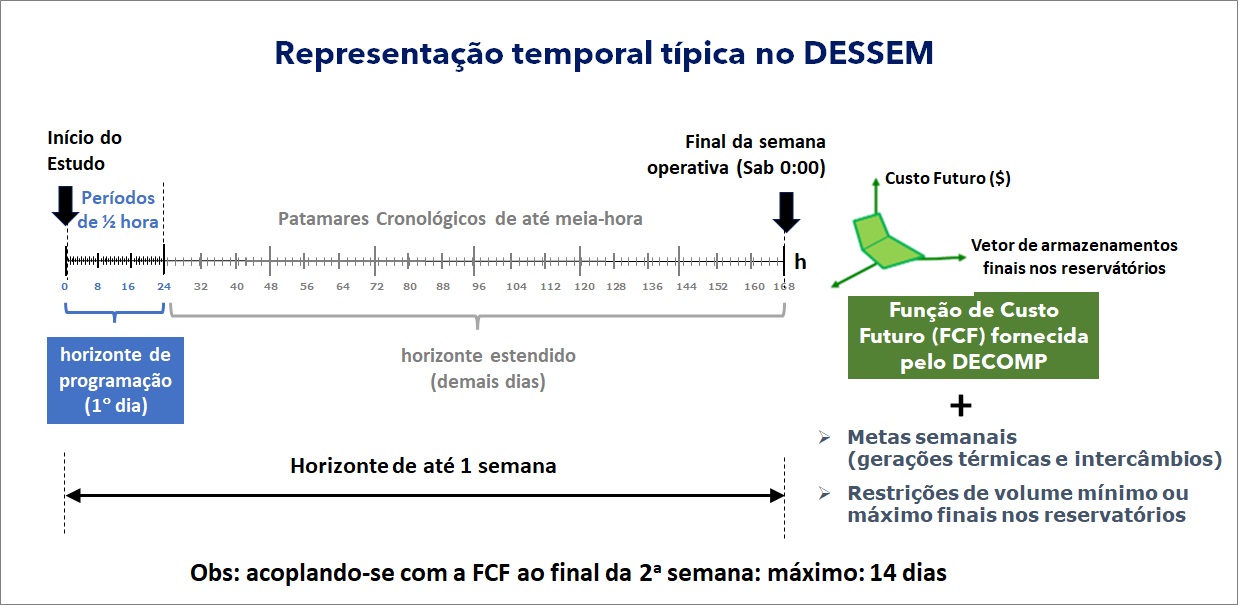
No uso prático para a programação da operação e formação de preços para o sistema brasileiro, ao executar o modelo DESSEM em um dia “D” do calendário civil, este horizonte de estudo é dividido tipicamente em duas partes, que são ilustradas na figura acima e descritas com mais detalhes a seguir:
horizonte de programação: corresponde à programação da operação para o dia seguinte (D+1), onde se adota, tipicamente, uma discretização semi-horária, a fim de se ter um refinamento adequado na operação e na determinação do preço. Como a execução do modelo é feita diariamente pelo ONS, este é o trecho do horizonte de estudo em que as decisões do modelo são efetivamente implementadas na prática;
um um horizonte estendido, que corresponde aos demais dias da semana até se atingir o final de uma sexta feira (ou seja, sábado às 0:00h), onde se obtém uma função de custo futuro (FCF) do modelo DECOMP. Neste horizonte, em geral adotam-se Períodos de tempo de maior duração, para diminuir o esforço computacional na resolução do problema.
Patamares Cronológicos¶
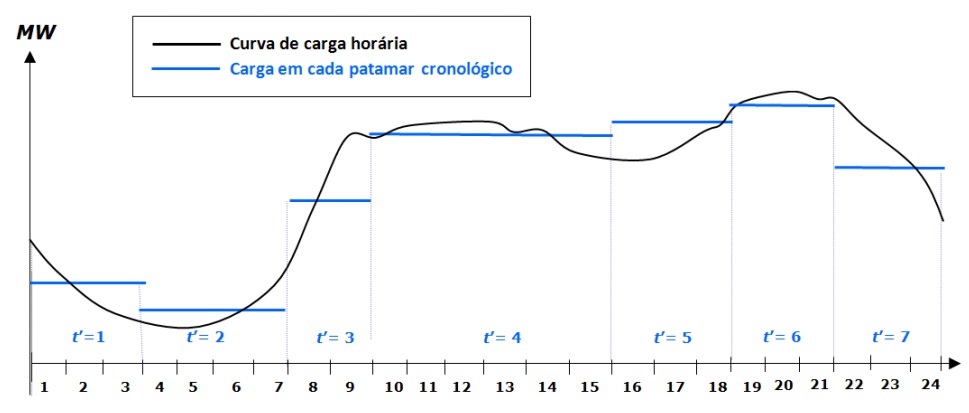
Os períodos que apresentam duração superior a meia ou 1 hora, situados em geral no horizonte estendido, são tipicamente denominados de “patamares cronológicos”. Nestes períodos, os dados do sistema seriam constituídos por uma média dos valores fornecidos nos dados de entrada ao longo das horas que constituem o patamar. Para o caso da carga, por exemplo, seria feita uma agregação da curva de carga horária em intervalos cronológicos superiores a uma hora, conforme mostra a figura a seguir.
Ressalta-se que o modelo não exige que os dados de entrada sejam informados na mesma escala temporal adotada para a representação de patamares cronológicos. Ou seja, pode-se informar, por exemplo, os dados em discretização horária ao longo de todo o horizonte de estudo, e o próprio modelo se encarrega de calcular os valores médios por período. Para maiores detalhes, consulte o Manual do Usuário do DESSEM. Já os resultados do modelo são publicados nos relatórios de saída sempre por período, portanto naturalmente já respeitarão a discretização temporal adotada.
É importante lembrar que, embora a definição dos patamares cronológicos seja fortemente guiada pela curva de carga, a utilização de patamares cronológicos no DESSEM não é equivalente, em termos de modelagem temporal, à representação de Patamares de Carga adotada nos modelos DECOMP e NEWAVE. A representação por patamares de carga nos modelos DECOMP/NEWAVE não possui sequência cronológica e pode incluir, em um mesmo patamar de carga, instantes de tempo que não estão temporalmente conectados. Para mais detalhes, consulte o Manual do modelo DECOMP.