Definições e Conceitos¶
Definimos como incerteza as grandezas que são utilizadas como dado de entrada nos modelos de otimização energética, mas cujos valores não podem ser determinados ou previstos com elevada precisão. Assim, é necessário tomar decisões levando em consideração diferentes possíveis valores para essas grandezas. De forma mais geral, quando um problema possui incertezas, diz-se que existe uma estocasticidade no problema.
Em princípio, a grande maioria dos dados de entrada do modelo são incertos, pois mesmo aqueles que são tomados como conhecidos podem sofrer variações em relação aos valores que são forecidos aos modelos. Entretanto, algumas dessas variações podem ser consideradas como sendo imprecisões, seja na determinação dos parâmetros dos componentes do sistema (como por exemplo o coeficiente mensal de evaporação de uma usina hidrelétrica) ou na medição desses valores, como o volume máximo de um reservatório. Tais valores devem ser considerados como valores conhecidos, ou seja, determinísticos.
Já para as grandezas que apresentam algum grau de incerteza não desprezível, deve-se fazer uma avaliação do custo-benefício de sua representação de forma explícita como uma variável incerta nos modelos, visto que isso acarreta, de forma geral, em aumento no custo computacional para resolver o problema, que muitas vezes pode ser significativa.
Desta forma, tendo em vista essa análise de custo-benefício, no problema de Planejamento Hidrotermo-eólico tratado nos modelos de otimização energética do CEPEL consideram-se, atualmente, as seguintes incertezas de forma explícita no problema de otimização, as quais são modeladas, portanto, como Variaveis aleatórias.
a Velocidade de vento e geração eólica dos parques eólicos.
Variaveis aleatórias¶
Um valor que é considerado incerto é denominado na literatura, de variável aleatória. Quando esses valores possuem uma dimensão superior a 1 (por exemplo, a incerteza nas vazões de várias usinas, ou na geração de vários parques eólicos), chamamos de vetor aleatório.
Tipos de variavel aleatória¶
É importante distinguir as variáveis aleatórias como sendo de dois tipos:
variáveis aleatórias discretas: são variáveis que assumem valores pontuais, ou seja, que podem ser “contados” (enumeráveis). Tem-se, como exemplo, a quantidade de falhas em uma unidade geradora ao longo de um mês. Ressalta-se que os valores de variável não necessariamente necessitam ser inteiros (embora na grande maioria das aplicações práticas o sejam) e nem consistir em um conjunto finito de valores;
variáveis aleatórias contínuas:: são variáveis que assumem valores ao longo de um intervalo, consistindo, portanto, de um conjunto não enumerável. É o exemplo, por exemplo, da vazão afluente a uma usina hidrelétrica, que pode assumir qualquer valor entre 0 e um valor máximo possível (que, em princípio, não precisa ser determinado).
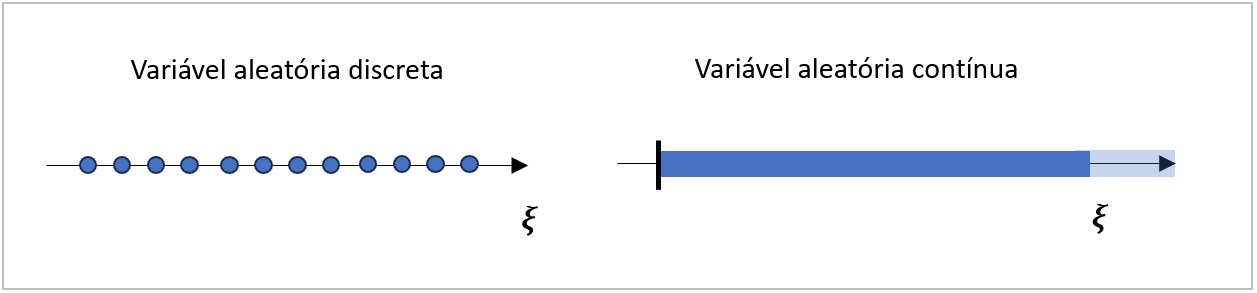
A figura a seguir ilustra o domínio de valores de uma variável aleatória \(\xi\) discreta (à esquerda) e contínua (à direita).
As incertezas atualmente representadas nos modelos de planejamento hidrotérmico, que correspondem às afluências as usinas hidrelétricas e a velocidade dos ventos nos parques eólicos, estão associadas a variáveis aleatórias contínuas.
Distribuição de probabilidades¶
A modelagem das incertezas nos modelos passa, inevitavelmente, pela representação matemática da variável aleatória (v.a.) associada a cada componente do vetor \(\xi\). Denomina-se distribuição de probabilidades à função que irá representar, do ponto de vista matemático, as seguintes informações para uma variável aleatória:
domínio de valores possíveis;
probabilidades associadas a cada valor ou intervalo de valores.
A modelagem da distribuição de probabilidades de uma variável aleatória contínua, que é o tipo de variável considerada nos modelos, é feita por meio da função densidade de probabilidade \(f(\xi)\), ilustrada a seguir, para o caso de uma variável aleatória que só assume valores positivos:
Nota
Conceitualmente, a função densidade de probabilidade \(f(\xi)\) pode ser entendida como sendo “o limite, quando o tamanho de intervalo de classe tende a zero, de um histograma de frequência relativa da variável aleatória, onde as frequências relativas são indicadas não nos valores do eixo 𝑦 (altura de cada barra), mas sim na área ocupada por cada barra”.
Por esse motivo, o cálculo das probabilidades, que é sempre feita em intervalos, corresponde à área abaixo da curva entre os pontos extremos do intervalo, como ilustrado na figura acima.
Ressalta-se que, por simplicidade de exposição, representou-se uma variável uni-dimensional, ou seja, \(\xi\) é um valor escalar (número real). Entretanto, no nosso problema de Planejamento Hidrotermo-eólico, a variável aleatória é multi-dimensional, o que levaria à modelagem de distribuições de probabilidades conjuntas para as várias componentes do vetor aleatório. As complexidades inerentes dessa modelagem multivariada são discutidas no Processo de Modelagem das Incertezas.
este é o Resultado do Teste
Teorema do Limite Central¶
Uma variável aleatória possui estatísticas (ex: valor esperado, desvio padrão) que podem ser obtidas de forma analítica a partir da Distribuição de probabilidades que foi considerada para modelá-la. O Teorema do Limite Central é uma ferramenta poderos para avaliar a aderência das estatísticas de uma amostra dessa variável aleatória em relação aos parâmetros da distribuição real, assim como a variabiidade dessas estatísticas em relação ao tamanho da amostra.
Este conceito, descrito a seguir, é bastante útil no processo de Avaliação da Acurácia da Modelagem tanto dos cenários gerados pelo Modelo GEVAZP, como dos resultados dos modelos NEWAVE e DECOMP ao utilizar esses cenários.
Processo Estocástico¶
O problema tratado nos modelos de planejamento é multi-estágio, ou seja, o Horizonte de Estudo é composto por diversos Períodos de tempo. Com isso, visto que as incertezas existem em todos os \(T\) períodos de tempo no futuro, introduz-se uma dimensão adicional ao vetor aleatório \(\xi\), que passa a ser representado da forma:
O conjunto \(\xi\) de todas essas variáveis aleatórias no tempo é o que se chama na literatura de processo estocástico.
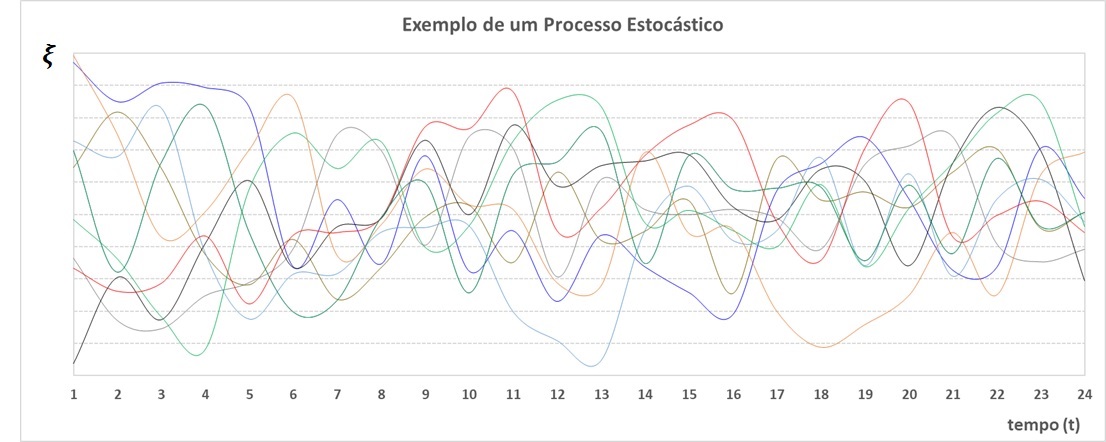
A figura a seguir ilustra um processo estocástico associado à geração de uma usina eólica, durante as 24 horas de um dia. Cada linha colorida indica uma possível realização para a geração dessa fonte ao longo do dia, sendo que as 10 curvas mostradas são apenas uma pequena amostra de todas as (infinitas) realizações que poderiam ter sido observadas. O conjunto de todas essas infinitas curvas é o que chamamos de processo estocástico.
Séries Temporais¶
Pode-se dizer que uma série temporal é uma realização amostral dentre todas as possíveis séries que poderiam ter sido geradas (ou observadas) em um Processo Estocástico. Portanto, a série temporal constitui-se em uma evolução, ao longo do tempo, de cada componente \(i\) do vetor aleatório, ou seja, \(\{\xi_i^t,t=1,\dots,T\}\). Por exemplo, pode-se ter uma série temporal referente à vazão afluente \(\{Qinc_i^t,t=1,\dots,T\}\) de uma usina hidrelétrica \(i\), ou a velocidade de vento \(\{Vel_i^t,t=1,\dots,T\}\) em um parque eólico \(i\), etc.
Para a construção do modelo estocástico, é importante conhecer os seguintes conceitos relacionadas ao estudo de séries temporais:
Tendência: indica o comportamento de longo prazo da série temporal, ou seja se os valores da variável possuem um comportamento de subida ou descida sistemático ao longo do tempo;
Sazonalidade: indica uma flutuação periódica na série temporal durante um determinado período, em geral, dentro do ano;
Ciclos: apresentam um comportamento similar aos comportamentos sazonais, porém com comprimento maior e sem duração uniforme;
Componente Aleatória (resíduo): procura capta todos os efeitos que não foram explicados pelos três componentes anteriores.
Em particular, o estudo da tendência leva aos seguintes conceitos adicionais:
Processo Estacionário: é aquele em que as propriedades estatísticas (distribuições de probabilidade) não variam ao longo do tempo, ou seja, são as mesmas para todos os intanstes de tempo \(t\), a menos de efeitos sazonais;
Processo estacionário de 2ª ordem: é um processo estacionário em que, além da média ser constante para cada instante de tempo, possui a seguintes características: - A variância para qualquer instnate \(t\) é constante; - a covariância entre variáveis de dois instantes de tempo \(\xi_t\) e \(\xi_{t+k}\) defasados do mesmo lag \(k\) é a mesma;
A avaliação de todas essas características de uma série temporal é feita a partir dos dados da Série Histórica da variável aleatória que está sendo observada.
Todos esses conceitos de series temporais serão utilizados, de uma forma ou outra, nos processos de Modelagem da incerteza hidrológica e Modelagem da incerteza dos Ventos.
Série Histórica¶
A série histórica é o registro de todos os valores observados no passado para a realização de uma variável aleatória. No contexto dos modelos energéticos, esta série consiste, por exemplo, de:
contunto de todas as vazões mensais observadas para as usinas hidrelétricas, desde quando se iniciou o processo de medição e registro das secao-series-historicas-vazoes;
conjunto de todas os valores horários de velocidade de vento registrados para os parques eólicos, ao longo do tempo.
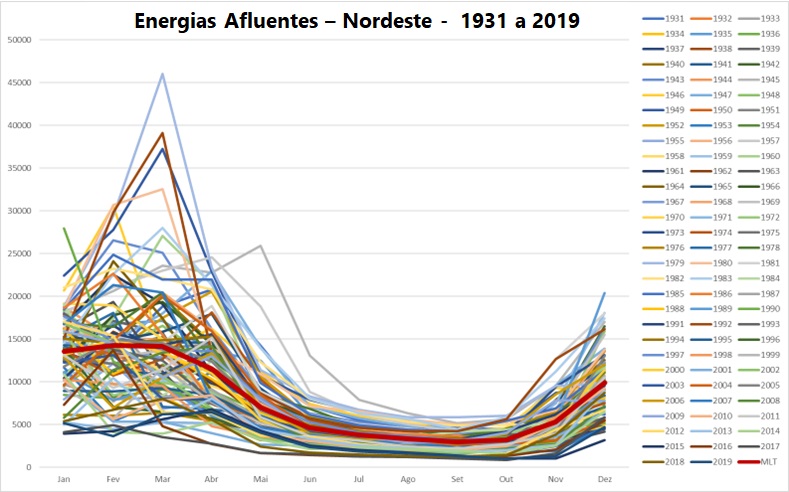
A figura abaixo ilustra um exemplo de série histórica.
Um conceitos fundamental para construção de um modelo estocástico a partir dos dados de uma série histórica é enunciado a seguir:
Ergodicidade: uma única realização da série temporal (na prática, a série histórica) é suficiente para obter todas as estatísticas da variável aleatória;
Portanto, é necessário estudar as propriedades estatísticas da série histórica de cada uma das componentes do vetor aleatório, com o objetivo de construir um modelo estocástico que possa descrever adequadamente a variável aleatória associada a cada componente. Assim, aplicando o conceito de ergodicidade, assume-se que a série histórica é apenas de um conjunto de todas as possíveis realizações que poderiam ter acontecido, e que constituem o processo estocástico como um todo. Assim, uma vez construído o modelo estocástico, aplicamos técnicas de Geração de cenários, com as quais obtê-se as chamadas séries sintéticas para o conjunto de variáveis aleatórias.
Conceitualmente, se o modelo estocástico está adequado, as séries sintéticas são indistinguíveis, do ponto de vista estatístico, da série histórica, e seu uso em modelos de programação estocástica permite que se consiga realizar uma análise mais diversificada e robusta do comportamento do sistema diante das incertezas.
Processo de Modelagem das Incertezas¶
No problema de Planejamento Hidrotermo-eólico considerado nos modelos de otimização energética, o vetor aleatório \(\xi\) possui as seguintes componentes:
\(\xi^t := \{Qinc_1^t,Qinc_2^t,\dots,Qinc_{NH}^t,Vel_1^t,Vel_2^t,\dots,Vel_{NEOL}^t\}\)
onde \(Qinc_i^t\) é a afluência natural a cada uma das \(NH\) usinas hidrelétricas e \(Vel_i^t\) é a velocidade do vento em cada um dos \(NEOL\) parques eólicos, para cada período de tempo.
Portanto, a rigor, será necessário modelar, para cada período \(t\) uma Distribuição de probabilidades conjunta para a variável aleatória multi-variada \(\{\xi_i, i=1,\dots, NH \times NEOL\}\), o que é uma tarefa bastante complexa. Além disso, a existência de dependência temporal faz com que, a rigor, tívessemos que representar a distribuição conjunta não só das variáveis em determinado período \(t\), mas também das variáveis pertencentes a todo o horizonte de estudo.
Entretanto, algumas características das variáveis aleatória e/ou da estratégia de solução permitem que se adote os seguintes procedimentos para a modelagem das variáveis aleatórias:
Como as variáveis aleatórias de diferentes naturezas (ex: afluências às usinas e velocidade de vento) possuem características estatísticas distintas, torna-se interessante utilizar modelos distintos para cada um desses conjuntos de variáveis;
Mesmo dentro de cada conjunto de variáveis aleatórias, torna-se interessante extrair a série temporal referente a cada componente \(i\) do vetor aleatório, que será calibrado separadamente.
Estes dois passos permitem, portanto, que seja feita, em um primeiro momento, uma modelagem individual para cada componente do vetor aleatório, ou seja, cada variável aleatória referente a determinado elemento do sistema (usinas hidrelérica ou parque eólico). Posteriormente, é levada em consideração a correlação espacial entre esses componentes, sejam de um mesmo tipo (correlação entre vazões de diferentes usinas ou ventos de diferentes parques eólicos) ou a correlação espacial entre as vazões afluentes e os ventos. Isto é necessário porque, conforme descrito na seção de secao-geracao-cenarios, em, um problema de otimização estocástica, cada cenário de incerteza a ser considerado nos modelos deve conter, de forma conjunta, valores para todos os componentes da variável aleatória.
Ainda que existam particularidades na Modelagem da incerteza hidrológica e Modelagem da incerteza dos Ventos., o processo geral de modelagem das incertezas de uma variável aleatória seguem os passos listados a seguir e descritos na sequência.
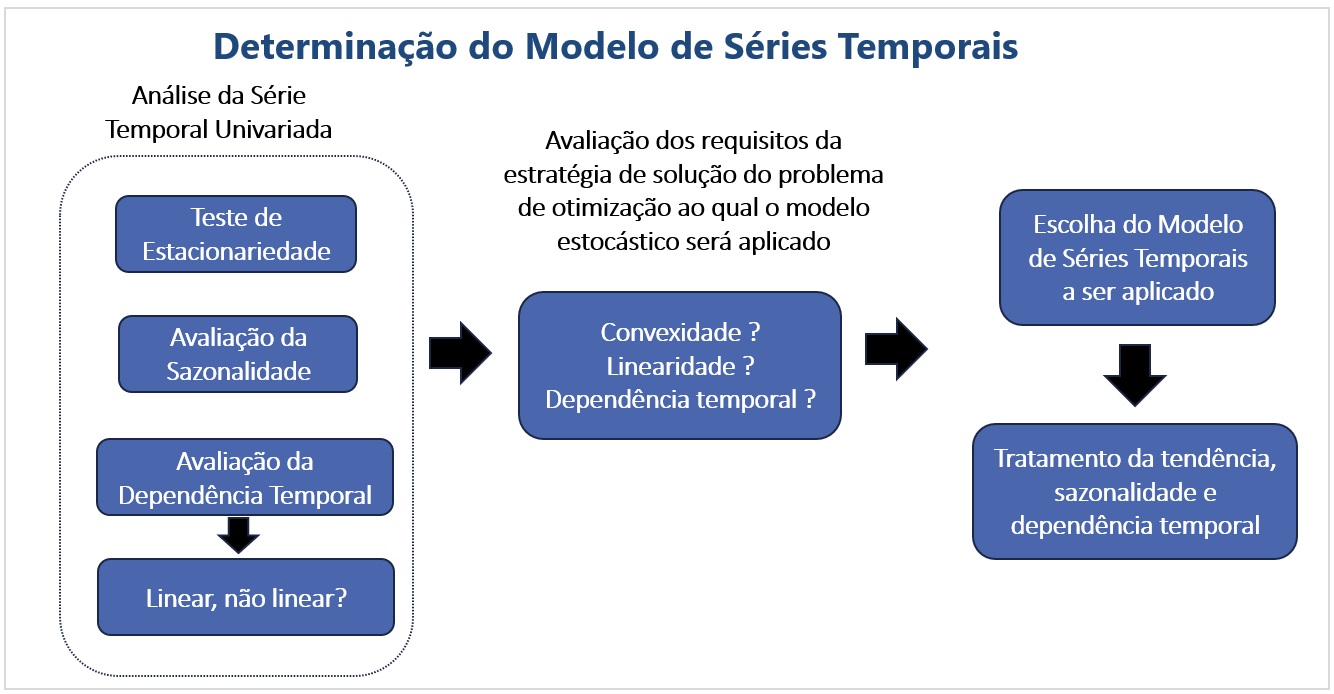
Avaliação do Modelo de Séries Temporais¶
A partir da série histórica individual para cada componente do vetor aleatório (usina hidrelétrica ou parque eólica), procede-se uma avaliação da série temporal, relacionada a esse componente, conforme mostrado a seguir.
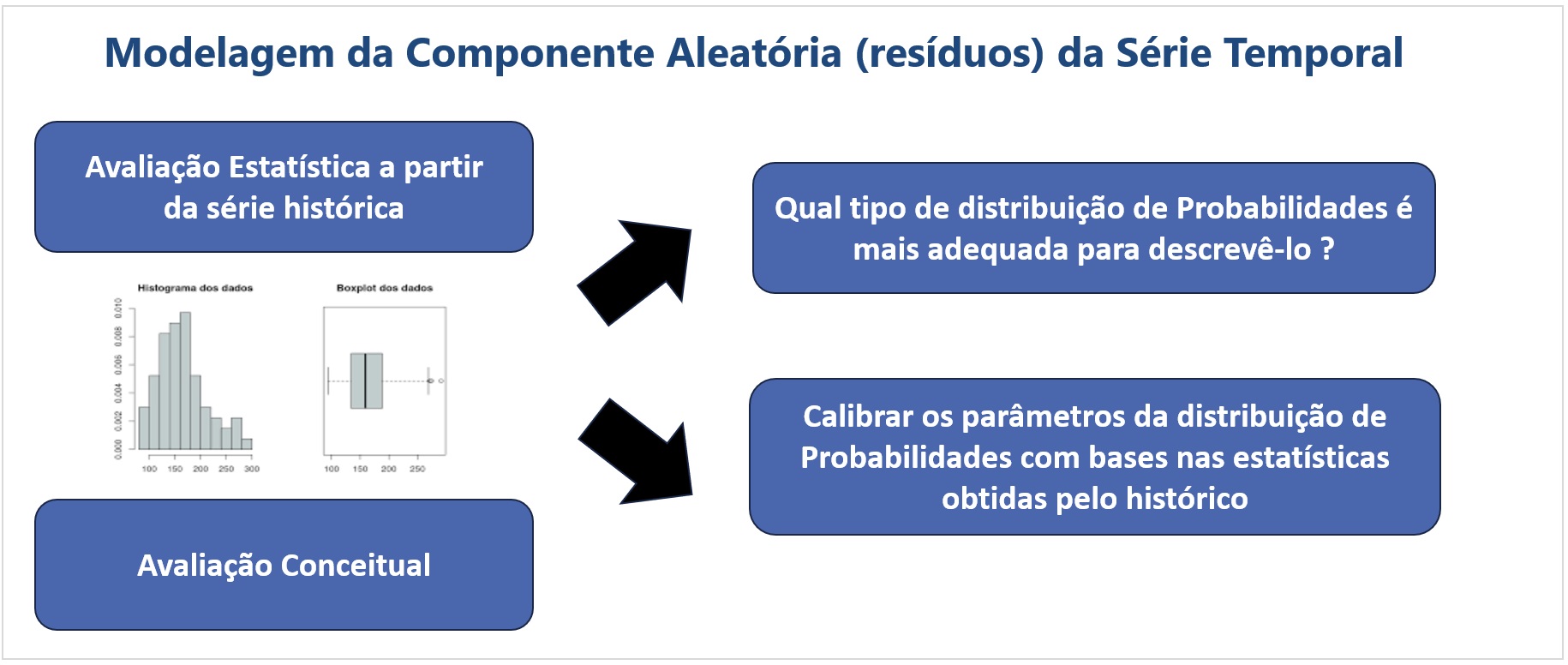
Avaliação da Distribuição dos resíduos¶
Uma vez extraída a sazonalidade, tendência (se for o caso) da série temporal, pode-se obter um processo estocástico estacionário, o qual, após ter sua eventual dependência temporal adequadamente tratada, possui um componente aleatório, que é denominado de resíduo. Este resíduo pode então ser modelado por uma Distribuição de probabilidades, utilizando os passos a seguir.
Tratamento da Correlação Espacial e Temporal¶
Uma vez aplicados os processos descritos nas seções acima, obtêm-se as determinadas as distribuições de probabilidades de cada componente do vetor aleatório, que são denominadas de distribuições de probabilidade marginais. As correlações cruzadas entre as variáveis aleatórias dentro de um mesmo período (correlação espacial) como em períodos distintos (correlação temporal) são tratados, de forma geral, como segue:
as correlações espaciais são introduzidas depois de sorteados o conjunto de resíduos para cada componente da variável aleatória, no processo de Geracao de Cenários;
as dependências temporais são introduzidas na formulaçãço matemática do problema de otimização, utilizando-se os parâmetros obtidos quando da calibração do modelo de série temporal para cada componente. Uma vez que o processo de decomposição temporal do problema faz com que as variáveis aleatórias de períodos diferentes se situam em subproblemas de otimização distintos, as variáveis aleatórias de determinado período \(t\) tornam-se variáveis de estado para os subproblemas dos períodos de tempo subsequentes.
Avaliação da Acurácia da Modelagem¶
Ao modelar qualquer Processo Estocástico que irá alimentar um modelo de otimização, como é o caso da Geração de Cenários feita pelo Modelo GEVAZP para os modelos NEWAVE, DECOMP e SUISHI, é fundamental avaliar a qualidade do modelo estatístico utilizado para representar do processo estocástico. Além disso, como em um secao-problema-otimizacao-estocastica é necessário discretizar as variáveis aleatórias contínuas, através da construção de uma Árvore de Cenários ou de geração de Séries sintéticas, é preciso, portanto, avaliar a qualidade dos resultados dos modelos de otimização ao se aplicar tal discretização.
Portanto, a avaliação do processo de representação das incertezas é feita em dois aspectos: na Qualidade dos cenários Gerados e Robustez e Estabilidade dos Resultados, que constituem, respectivamente os dados de entrada e resultados dos modelos de otimização. Assim, o primeiro aspecto visa avliar o modelo GEVAZP e, o segundo, os modelos NEWAVE e DECOMP.
Os tipos de análises descritos a seguir são realizadas de forma bastante rigorosa pelas instituições do setor elétrico (ONS, CCEE e EPE), o que atesta a qualidade dos resultados dos modelos. Muitos dos testes estatísticos para avaliação do modelo GEVAZP já são realizados pelo próprio modelo, que emite relatórios de saída para análise do usuário. Já as análises referentes aos modelos NEWAVE e DECOMP requerem um esforço bem maior de realização, pois envolvem uma quantidade muito grande execuções dos modelos, variando a semente e/ou a quantiade de Aberturas a serem utilizadas em cada período de tempo na discretização temporal dos modelos.
Qualidade dos cenários Gerados¶
Neste aspecto, avalia-se a qualidade e robustez dos cenários que representam o processo estocástico tratado pelos modelos, o que compreende uma avaliação estatística dos cenários gerados para a variável aleatória, para verificar se:
representam de forma adequada a Distribuição de probabilidades que foi concebida para modelar a variável aleatória. Assim, é preciso avaliar se as propriedades estatísticas destes cenários representam adequadamente a distribuição, cujos parâmetros são conhecidos, já que são frutos do processo de calibração dos modelos (vide as seções de Distribuição Lognormal 3 parâmetros e estimação dos parâmetros do Modelo Par(p));
apresentam uma robustez adequada em relação à variabilidade intrínseca do processo de geração de cenários quando se varia a semente utilizada para gerar os cenários.
Para ambos os tipos de análise, é fundamental lançar mão do Teorema do Limite Central, para avaliar a aderência entre os parâmetros avaliados nos cenários (média, variância, assimetria, etc,) e os valores assumidos no modelo teórico. Esta análise envolve construção de intervalos de confiância para os valores dos parâmetros e a aplicação de testes estatísticos para aferir a aderência entre as distribuições.
Os cenários também devem ser avaliados para verificar se:
representam, de forma adequada, a variável aleatória “real” cujos parâmetros são, em principio, desconhecidos, e da qual temos apenas uma amostra, dada pela Série Histórica.
Esta última análise é feita aplicando-se diversos testes estatísticos para avaliar se os cenários gerados representam adequadamente a série histórica.
Em resumo, nas duas primeiras análises mais acima, estamos preocupados em avaliar se o processo de Geração de Cenários foi feito de forma adequada, a partir do modelo escolhido para a variável aleatória e do tamanho da Árvore de Cenários utilizada. Já nessa terceira análise verificamos se os próprios modelos escolhidos para representar a incerteza hidrológica e da incerteza eólica estão adequados, tomando como evidência para essa comparação os cenários gerados..
Robustez e Estabilidade dos Resultados¶
Nesta análise, avalia-se a qualidade e robustez dos resultados obtidos pelos modelos NEWAVE e DECOMP (custo marginal de operação, o risco de déficit, etc.), a partir dos cenários construídos para as variáveis aleatórias. Ou seja, não é suficiente analisar os cenários gerados, sendo também preciso avaliar o efeito que eles tem nos resultados, verificando, por exemplo,
se variações na semente utilizadas na geração de cenários não causam variações muito grandes - ou não explicáveis - nos resultados;
se pequenas variações em alguns parâmetros do processo (por exemplo, quantidade de cenários gerados) também não causam perturbações excessivas nos resultados. Ressalta-se que, em relação a esse segundo aspecto, deve-se levar em consideração o custo-benefício, visto que uma maior quantidade de cenários leva, em geeral, a aumentos no tempo computacional.
Nesta análise, também é fundamental lançar mão do Teorema do Limite Central, aplicando-o junto com os estudos sobre o que se chama, em programação estocástica, de secao-sample-average-approximation.