Motivação

Para resolução dos secao-problema-otimizacao-estocastica oriundos do Planejamento Hidrotermo-eólico como é impossível resolver o secao-problema-real-estocástico com a Distribuição de probabilidades contínua para as variáveis aleatórias (ou, em uma descrição mais precisa, o vetor aleatório), é necessário aproximá-la através de uma discretização em um conjunto finito de valores possíveis, que dão origem ao secao-problema-arvore-completa.

Estes cenários, ilustrados a seguir, são utilizados para representar as incertezas no problema estocástico que é resolvido para o Modelo NEWAVE, para o planejamento a médio e longo prazos, e o modelo Modelo DECOMP, para o planejamento de curto prazo do Sistema Interligado Nacional (SIN).

Em geral, os resultados do problema de otimização e a política operativa que é obtida dependem fortemente dos cenários gerados. Quanto maior o tamanho da árvore, mais bem representada estará a variável aleatória, porém o custo computacional para resolução do problema aumenta, por vezes de forma significativa. Assim, na geração desta árvore de cenários deve ser avaliado o custo X benefício do tamanho da árvore em cada período, em termos de acurácia na modelagem das incertezas X tempo de resolução do problema.

Também é importante gerar séries sintéticas para estudos de simulação hidrotérmo-eólica, onde, tipicamente, avaliamos o desempenho de determinada política calculada pelo problema de otimização.

Em geral, há grande escalabilidade do tempo computacional em relação à quantidade de séries que são geradas para os modelos SUISHI ou simulações finais com o NEWAVE, visto que, * como a política operativa já está obtida, as simulações em cada série são independentes, podendo-se desta forma, fazer um uso mais efetivo do processamento paralelo.

Objetivos

Os principais objetivos a serem atingidos pelas técnicas de geração de cenários são:

• Representar da melhor forma possível as propriedades da da variável aleatória, com um determinada quantidade limitada de cenários. Em princípio, deve-se procurar representar da melhor forma possível a Distribuição de probabilidades da variável aleatória, como ilustrado abaixo

• Possuir baixa variabilidade nos resultados, ao se modificar alguns dos parâmetros do algoritmo, como por exemplo a “semente” para geração de números aleatórios (redução da variância);

• Aproximar da melhor forma a solução ótima (decisões e custo) do problema contínuo 1, procurando refinar a discretização da variável aleatória em regiões onde elas possuem mais impacto nos resultados do problema 2.

Definições

O processo de geração de cenários dá origem a algumas definições (“jargões”), utilizadas ao longo dessa documentação, que são ilustrados na figura abaixo e descritos a seguir.

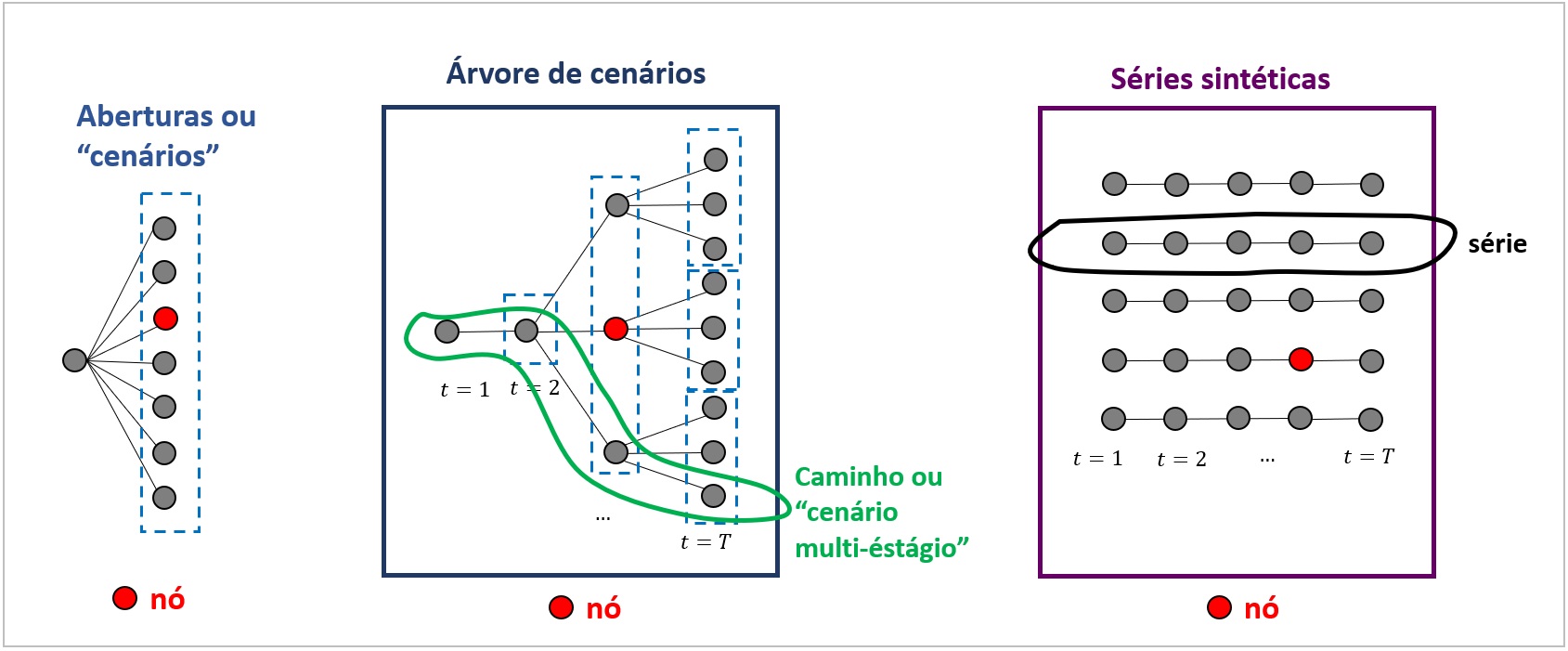
Aberturas

Consiste em um conjunto de valores da variável aleatória para determinado período, gerados a partir de uma representação determinística ou estocástica dos períodos anteriores;

Árvore de Cenários

Consiste na combinação das aberturas consideradas em diferentes períodos de tempo, que são encadeadas de forma sucessiva.

Nesta árvore podemos definir os seguintes elementos:

• caminho da árvore: consiste, literalmente, em um “caminho” que se percorre na árvore de cenários, desde o seu período inicial até o seu período final.

• nós: consiste nos “pontos” que são produzidos em uma árvore de cenários (quando se realizam aberturas) ou em um conjunto de séries, quando se seleciona uma série e um período.

Séries sintéticas

Do ponto de vista conceitual, é semelhante ao caminho em uma Árvore de Cenários, porque consiste em uma combinação de valores da variável aleatória em cada período de tempo, A distinção que se faz é que não há, de forma explícita, uma árvore de cenários da qual se extraiu essa série, ou seja, são geradas “livremente”.

Semente

Em um processo de geração de cenários, a “semente aleatória (ou simplesmente semente) é um número utilizado para iniciar um algoritmo gerador de números aleatórios, que é utilizado por métodos de geração de cenários. Ou seja, diferentes execuções de um mesmo algoritmo para geração de números aleatórios resulta na obtenção de sequências diferentes de números aleatorios.

Como os métodos de geração de cenários dependem da geração de números aleatórios, os cenários gerados acabam dependendo da semente escolhida.

Para atender aos requisitos de reprodutibilidade dos resutlados, ou seja, diferentes execuções dos modelos produzirem sempre o mesmo resultado, é necessário fixar a semente que é utilizada nos métodos de Amostragem Aleatória Simples (AAS) e Amostragem Seletiva (AS) utilizada pelo GEVAZP.

Entretanto, durante os processos de validação dos modelos junto às instituições e com participação dos agentes, permite-se que a semente seja um dado de entrada do modelo, de forma a permitir que se avalie de forma mais adequada a Avaliação da Acurácia da Modelagem das variáveis aleatórias, assim como a estabilidade e robustez dos resultados ao se variar a semente.

Métodos de Geração de Cenários

Diversos métodos de geração de cenários tem sido propostos na literatura. A seguir, descrevemos brevemente alguns métodos mais clássicos que são adotados. Para uma revisão bibliográfica mais ampla até os anos 2000 sugerimos a referência 3, e para uma revisão mais atual, aplicada para sistemas de potência, a referência 4.

Amostragem Aleatória Simples

Este é o método mais simples de geração de cenários, que consiste em sortear, aleatoriamente, valores equiprováveis da Distribuição de probabilidades da variável aleatória 5. Para uma variável aleatória univariada, os valores podem ser obtidos sorteando valores de uma distribuição uniforme entre 0 e 1 13, e aplicando-se a inversa da função de distribuição acumulada, como ilustrado na figura a seguir.

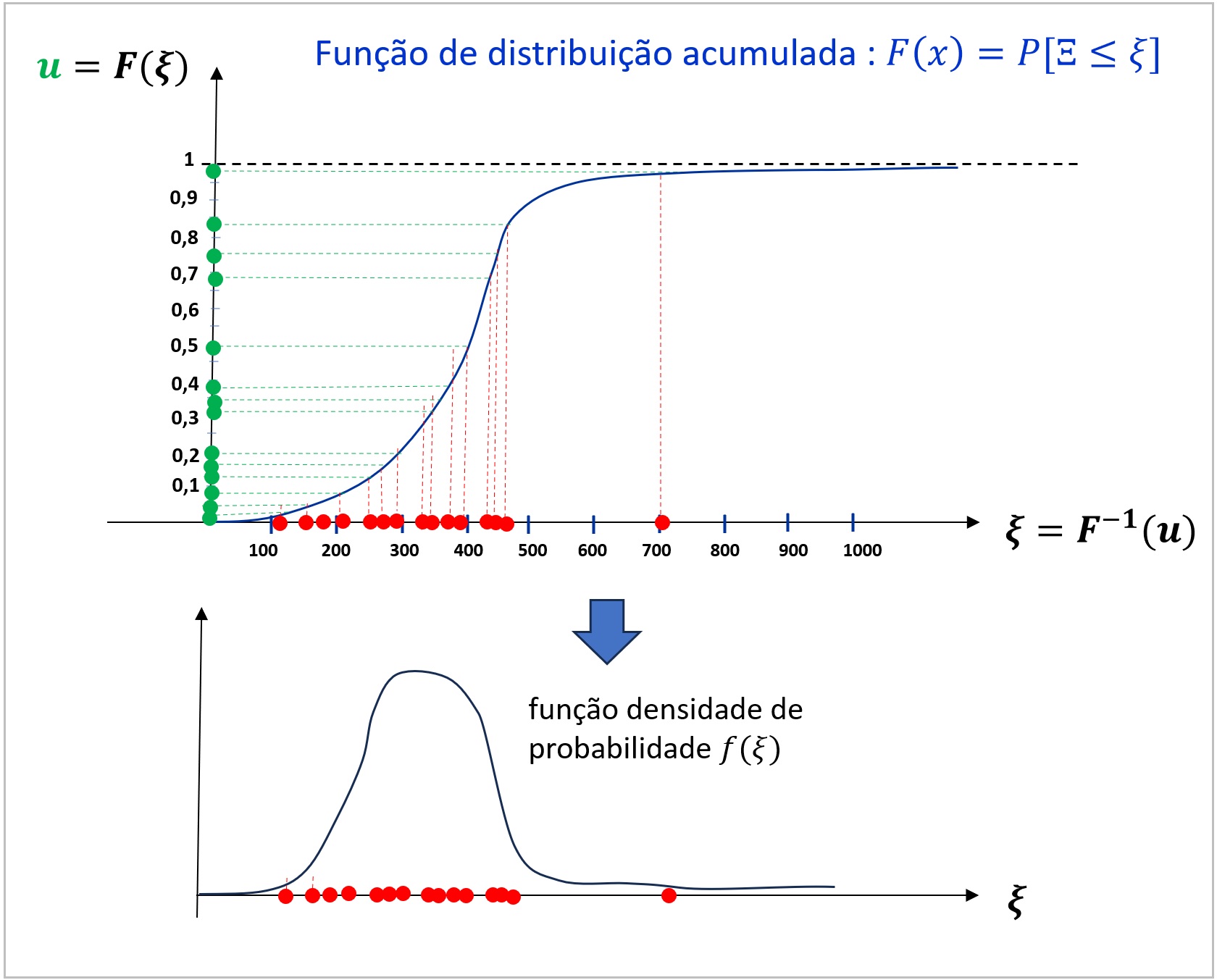
Uma deficiência importante do método de amostragem aleatória simples, quando aplicado para geração de cenários para a resolução de um problema estocástico, é apresentar uma variabildiade potencialmente grande dos cenários com a semente escolhida. Isso acaba resultando na necessidade de se ter uma maior quantidade de cenários para se ter robustez nos resultados. Por esse motivo, o método de AAS não é recomendado para geração dos cenários backward do NEWAVE, ou para construir a árvore de cenários do DECOMP, mas apenas para gerar cenários para a simulação fina do NEWAVE, ou simulações com o modelo SUISHI.

Para esses processo, recomenda-se utilizar métodos que apresentam menor variância, como os mostrados a seguir.

Método k-Means

O algoritmo k-means é uma técnica de clusterização que procura agrupar \(M\) pontos inciais, com dimensão \(n\), em \(K\) objetos, com base nas distãncias entre os pontos. O objetivo é minimizar a soma dos quadrados das distâncias entre os objetos no mesmo grupo. A figura a seguir, extraída do endereço https://medium.com/@englucsantosilva/algoritmo-k-means-na-pr%C3%A1tica-75f4ca656bbc ilustra o algoritmo:

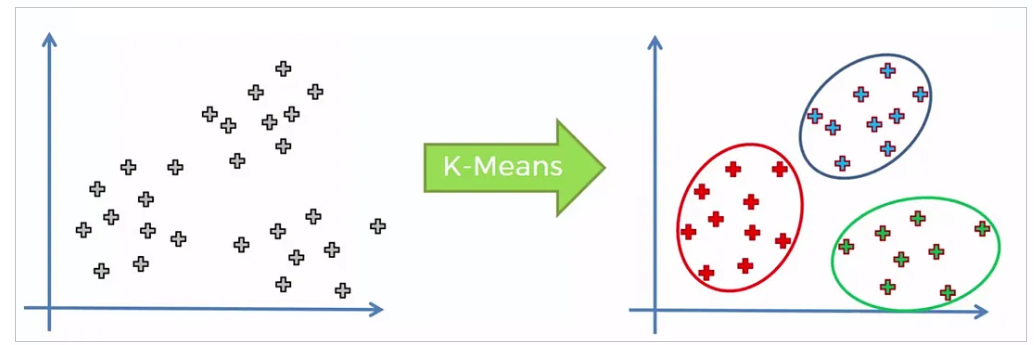
O representante de cada grupo pode ser o centróide ou, caso se deseje utilizar como representante um ponto que foi de fato gerado originalmente, pode-se escolher o ponto mais próximo do centróide. Uma análise comparativa dessas alternativas, mostrando algumas vantagens de se utilizar o centróide é apresentada em 6, 7.

O algoritmo k-means é a base da estratégia de Amostragem Seletiva (AS), que é utilizado pelo modelo GEVAZP na geração dos cenários backward do NEWAVE, assim como na geração de cenários para o modelo DECOMP. A principal vantagem desse método é promover uma grande redução na variabilidade dos resultados do método de amostragem aleatória simples, visto que, como o conjunto de pontos inciais é muito grande, fica-se pouco suscetível a variações no valor da semente.

Quasi Monte-Carlo (QMC)

O método de Quasi Monte-Carlo (QMC) 8 visa suprir uma deficiência dos métodos de amostragem simples, ao utilizar, ao invés de valores sorteados aleatoriamente, pontos escolhidos de forma mais adequada, que resultam em low discrepancy sequences. Em outras palavras, este método reduz a variância do método de Amostragem Aleatória Simples, acelerando sua convergência com o aumento do tamanho da amostra.

Este método foi aplicado ao problema de planejamento hidrotérmico resolvido por PDDE em 9.

Fonte: 9

Hipercubo Latino (LHS)

É um método de amostragem estratificada, proposto em 10 e cujas boas propriedades para amostras grandes é discutida em 11. Consiste em uma repartição do domínio da variável aleatório em “cubos” com dimensão igual ao da variável, procurando amostrar valores de maneira uniforme ao longo do domínio. Ou seja, procura-se sortear, para cada dimensão da variável aleatória, um valor dentro de cada intervalo ao qual o domínio nesta dimensão é dividido. A combinação entre os valores das diferentes componentes deve ser feita de for a melhor representar a correlação espacial.

Assim, ao mesmo tempo em que se varre de forma mais ampla o domínio da variável, o que pode ser considerada uma limitação do método de Método k-Means (pelo fato de este consierar o centróide de cada grupo), garante-se uma maior estabilidade à variação da semente.

A figura a seguir ilustra o princípio adotado por esse método.

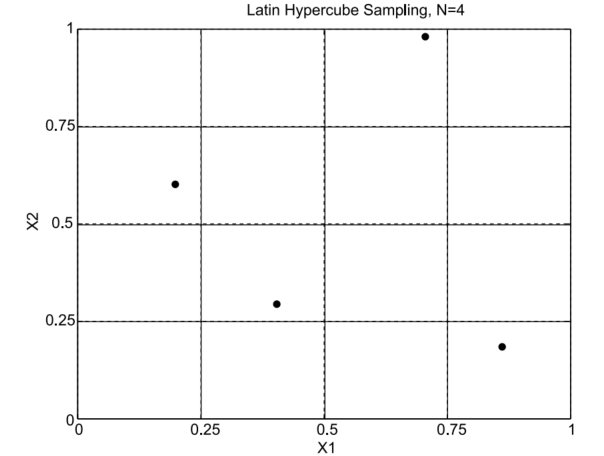
Fonte: 9

A maior dificuldade deste método é garantir uma distribuição adequada desses pontos, para variáveis aleatórias com dimensões muito elevadas.

Aplicações desse método ao problema de planejamento hidrotérmico podem ser encontradas em 9, 12.

Referências

1

M. Casey and S. Sen. The scenario generation algorithm for multistage stochastic linear programming. Mathematics of Operations Research, 30(3):615–631, 2005.

2

M. A. H. Dempster and R. T. Thompson. Evpi-based importance sampling solution proceduresfor multistage stochastic linear programmeson parallel mimd architectures. Annals of Operations Research, 90:161–184, 1999. doi:10.1023/A:1018956530304.

3

Jitka Dupačová, Giorgio Consigli, and Stein W. Wallace. Scenarios for multistage stochastic programs. Annals of Operations Research, 100(1):25–53, 2000. doi:10.1023/A:1019206915174.

4

Hui Li, Zhouyang Ren, Miao Fan, Wenyuan Li, Yan Xu, Yunpeng Jiang, and Weiyi Xia. A review of scenario analysis methods in planning and operation of modern power systems: methodologies, applications, and challenges. Electric Power Systems Research, 205:107722, 2022. doi:https://doi.org/10.1016/j.epsr.2021.107722.

5

Sarjinder Singh. Simple Random Sampling, pages 71–136. Springer Netherlands, Dordrecht, 2003. doi:10.1007/978-94-007-0789-4_2.

6(1,2)

D. D. J. Penna, F. Treistman, and M. E. P. Maceira. Avaliação de alternativas para escolha do representante no processo de agregação da amostagem seletiva. Relatório Técnico 13612-2018, CEPEL - Centro de Pesquisas de Energia Elétrica, 2018.

7

F. Treistman, L. C. Brandão, D. D. J. Penna, M. E. P. Maceira, and H. S. Araújo. Avaliação do uso do centroide no processo de agregação da amostragem seletiva na geração de cenários de afluências para o planejamento da operação de curto prazo. Relatório Técnico 3383/2019, CEPEL - Centro de Pesquisas de Energia Elétrica, 2019.

8

R. Niederreiter. Random Number Generation and Quasi-Monte Carlo Methods. SIAM, Philadelphia, 1992.

9(1,2,3,4)

T. Homem-de-Mello, V. L. de Matos, and E. C. Finardi. Sampling strategies and stopping criteria for stochastic dual dynamic programming: a case study in long-term hydrothermal scheduling. Energy Systems, 2:1–31, 2011.

10

M. D. Mckay, R. J. Beckman, and W. J. Conover. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics, 21(2):239–245, 1979.

11

Michael Stein. Large sample properties of simulations using latin hypercube sampling. Technometrics, 29(2):143–151, 1987.

12

Xiaolin Ge, Shu Xia, and Wei-Jen Lee. An efficient stochastic algorithm for mid-term scheduling of cascaded hydro systems. Journal of Modern Power Systems and Clean Energy, 7(1):163–173, 2019. doi:10.1007/s40565-018-0412-6.

13

este sorteio pode ser realizado utilizando a função “ALEATORIO()” no Microsoft Excel.

Etapas do Processo

Nota

Volte mais tarde ou consulte os relatórios técnicos do CEPEL que descrevem as funcionalidades e os manuais já existentes em pdf dos modelos, que estão disponíveis para download público no seguinte endereço: (https://www.cepel.br/produtos/documentacao-tecnica/)

Dúvidas? Contacte as equipes dos modelos: newave@cepel.br; decomp@cepel.br; dessemp@cepel.br; gevazp@cepel.br; suishi@cepel.br; previvaz@cepel.br

Geração dos ruídos

Nota

Volte mais tarde ou consulte os relatórios técnicos do CEPEL que descrevem as funcionalidades e os manuais já existentes em pdf dos modelos, que estão disponíveis para download público no seguinte endereço: (https://www.cepel.br/produtos/documentacao-tecnica/)

Dúvidas? Contacte as equipes dos modelos: newave@cepel.br; decomp@cepel.br; dessemp@cepel.br; gevazp@cepel.br; suishi@cepel.br; previvaz@cepel.br

Amostragem Seletiva (AS)

Atenção

Enquanto esta página não está pronta, você pode consultar o material sobre Amostragem Seletiva nos relatórios técnicos 6, 14 e artigos 15, 16 do CEPEL sobre essa funcionalidade.

Referências

14

D. D. J. Penna, M. E. P. Maceira, and J. M. Damázio. Definição da árvore de cenários de afluências para o planejamento da operação energética de médio prazo. Relatório Técnico 46994/2009, CEPEL - Centro de Pesquisas de Energia Elétrica, 2009.

15

M. E. P. Maceira, D. D. J. Penna, A. L. Diniz, R. J Pinto, A. C. G. Melo, C. V Vasconcellos, and C. B. Cruz. Twenty years of application of stochastic dual dynamic programming in official and agent studies in brazil - main features and improvements on the newave model. In 20th PSCC - Power Systems Computation Conference. Dublin, Ireland, June 2018.

16

D. D. J. Penna, M. E. P. Maceira, and J. M. Damázio. Selective sampling applied to long-term hydrothermal generation planning. In 17th Power Systems Computaion Conference. 2011.

Amostragem Aleatória Simples (AAS)

Nota

Volte mais tarde ou consulte os relatórios técnicos do CEPEL que descrevem as funcionalidades e os manuais já existentes em pdf dos modelos, que estão disponíveis para download público no seguinte endereço: (https://www.cepel.br/produtos/documentacao-tecnica/)

Dúvidas? Contacte as equipes dos modelos: newave@cepel.br; decomp@cepel.br; dessemp@cepel.br; gevazp@cepel.br; suishi@cepel.br; previvaz@cepel.br

Geração de Árvore de Cenários

Para a etapa “backward” de cálculo da política no modelo NEWAVE (Modelo de Planejamento da Operação de Sistemas Hidrotérmicos Interligados de Longo e Médio-Prazo) e para o modelo DECOMP (Modelo de Planejamento da Operação de Sistemas Hidrotérmicos Interligados de Curto Prazo) é necessária a construção de uma árvore de cenários, composta de um conjunto de possíveis realizações das incertezas em cada período de tempo e que, devido à correlação temporal, dependem das realizações passadas a cada cenário.

A construção destes cenários é feita utilizando-se o modelo Par(p) 17, que a partir de 2020 também permite considerar, além das correlações mensais, a vazão média nos últimos doze meses também como variável de estado (modelo Par(p)-A) 1819. Com isso, consegue-se representar melhor a persistência de séries críticas de maior duração, que vêm sendo observadas recentemente no sistema brasileiro. Para aferir a qualidade dos cenários que são gerados, uma série de análises estatísticas são realizadas. 20

Em virtude de restrições de tempo computacional para resolução do problema de otimização estocástica nos modelos de planejamento da operação, o modelo GEVAZP utiliza o método de amostragem seletiva, que possibilita representar, de forma adequada, o processo estocástico de vazões/energias com um reduzido número de cenários. A amostragem seletiva consiste em aplicar técnicas de clusterzização a um grande número de cenários hidrológicos gerados, de forma a escolher um conjunto representativo a partir da amostra original de cenários.

Os cenários hidrológicos utilizados nos modelos de planejamento da operação de médio e curto prazos são gerados levando-se em consideração a preservação das características estatísticas do processo estocástico original, como média, variância, correlações temporais e espaciais das vazões, regras operativas, registros de vazão incremental bem como informação macroclimática (Oceanic Niño Index ONI) com o objetivo de capturar a influência do El Niño – Oscilação Sul (ENOS) sobre a precipitação em diversas regiões do Brasil, o que impacta diretamente nos regimes hidrológicos e na geração de energia do país. 21, 22.

Apresenta-se a seguir um esquema ilustrativo do conjunto de cenários que é gerado para o DECOMP (à esquerda) e para o NEWAVE (à esquerda). Na resolução do problema pelo DECOMP, todos os arquivos são percorridos, aplicando-se a técnica de programação dinâmica dual (PDD). Já o NEWAVE percorre a árvore de cenários de forma amostral, em virtude da enorme quantidade de cenários para o problema como um todo, que corresponde a todas as combinações possíveis entre as aberturas de cada período.

O modelo GEVAZP também permite o cálculo das vazões afluentes para postos de vazão artificial e postos de vazão incremental.:footcite:2016-TreistmanAraujoPennaMaceira_RelTecCEPEL-27063_GeracaoCenarios-VazoesLaterais-Postos-Artificiais-GEVAZP Postos de vazão artificial são aqueles que possuem regras operativas próprias, inseridas como dados de entrada ao modelo, em geral associadas a postos de vazão natural. Para casos onde o tempo de viagem da água entre duas usinas é significativo, permite-se adotar diretamente o registro de vazão incremental para a usina impactada pelo tempo de viagem.

Geração de Séries Sintéticas

Ainda em relação ao modelo NEWAVE e também para o modelo SUISHI (Modelo de Simulação a Usinas Individualizadas de Subsistemas Hidrotérmicos Interligados), é necessária a realização de simulações com um grande número de cenários hidrológicos, visando a escolha de estados para a construção da função de custo futuro (na etapa forward do NEWAVE) e para calcular índices probabilísticos de desempenho do sistema para cada estágio da simulação (no modelo SUISHI e simulação final do NEWAVE).

Geração de Séries Sintéticas Condicionadas

Nota

Volte mais tarde ou consulte os relatórios técnicos do CEPEL que descrevem as funcionalidades e os manuais já existentes em pdf dos modelos, que estão disponíveis para download público no seguinte endereço: (https://www.cepel.br/produtos/documentacao-tecnica/)

Dúvidas? Contacte as equipes dos modelos: newave@cepel.br; decomp@cepel.br; dessemp@cepel.br; gevazp@cepel.br; suishi@cepel.br; previvaz@cepel.br

Geração de cenários de ventos

Em relação à modelagem da incerteza dos aproveitamentos eólicos, o modelo GEVAZP propõe uma abordagem para a modelagem de velocidades mensais de ventos por meio de distribuições Weibull tri-paramétricas para a geração de cenários de ventos mensais correlacionados com vazões às usinas hidroelétricas. 23, 24.

A velocidade dos ventos é modelada como uma regressão das afluências mais um resíduo. Assim, a distribuição Weibull é ajustada aos resíduos das velocidades mensais de ventos, normalmente distribuídos e que guardam as correlações cruzadas entre hidroelétricas e parques eólicos. A abordagem proposta busca preservar a média, o desvio-padrão e, especialmente, a assimetria das velocidades históricas dos ventos mensais, sendo particularmente adequada em situações de assimetrias elevadas.

Os cenários de velocidade de ventos são gerados a partir de uma agregação das usinas eólicas em parques elólicos equivalentes (PEEs) e considerando a correlação espacial com as vazões afluentes às usinas hidrelétricas. Assim, modela-se a distribuição conjunta dos cenários de vazões e ventos, ilustrada na figura a seguir e descrita com mais detalhes em 25, 26, 27.

.

Avaliação dos Cenários Gerados

Nota

Volte mais tarde ou consulte os relatórios técnicos do CEPEL que descrevem as funcionalidades e os manuais já existentes em pdf dos modelos, que estão disponíveis para download público no seguinte endereço: (https://www.cepel.br/produtos/documentacao-tecnica/)

Dúvidas? Contacte as equipes dos modelos: newave@cepel.br; decomp@cepel.br; dessemp@cepel.br; gevazp@cepel.br; suishi@cepel.br; previvaz@cepel.br

Cenários em Pente (séries)

Nota

Volte mais tarde ou consulte os relatórios técnicos do CEPEL que descrevem as funcionalidades e os manuais já existentes em pdf dos modelos, que estão disponíveis para download público no seguinte endereço: (https://www.cepel.br/produtos/documentacao-tecnica/)

Dúvidas? Contacte as equipes dos modelos: newave@cepel.br; decomp@cepel.br; dessemp@cepel.br; gevazp@cepel.br; suishi@cepel.br; previvaz@cepel.br

Cenários em Árvore

Nota

Volte mais tarde ou consulte os relatórios técnicos do CEPEL que descrevem as funcionalidades e os manuais já existentes em pdf dos modelos, que estão disponíveis para download público no seguinte endereço: (https://www.cepel.br/produtos/documentacao-tecnica/)

Dúvidas? Contacte as equipes dos modelos: newave@cepel.br; decomp@cepel.br; dessemp@cepel.br; gevazp@cepel.br; suishi@cepel.br; previvaz@cepel.br