Métodos de Geração de Cenários

Diversos métodos de geração de cenários tem sido propostos na literatura. A seguir, descrevemos brevemente alguns métodos mais clássicos que são adotados. Para uma revisão bibliográfica mais ampla até os anos 2000 sugerimos a referência 1, e para uma revisão mais atual, aplicada para sistemas de potência, a referência 2.

Amostragem Aleatória Simples

Este é o método mais simples de geração de cenários, que consiste em sortear, aleatoriamente, valores equiprováveis da Distribuição de probabilidades da variável aleatória 3. Para uma variável aleatória univariada, os valores podem ser obtidos sorteando valores de uma distribuição uniforme entre 0 e 1 11, e aplicando-se a inversa da função de distribuição acumulada, como ilustrado na figura a seguir.

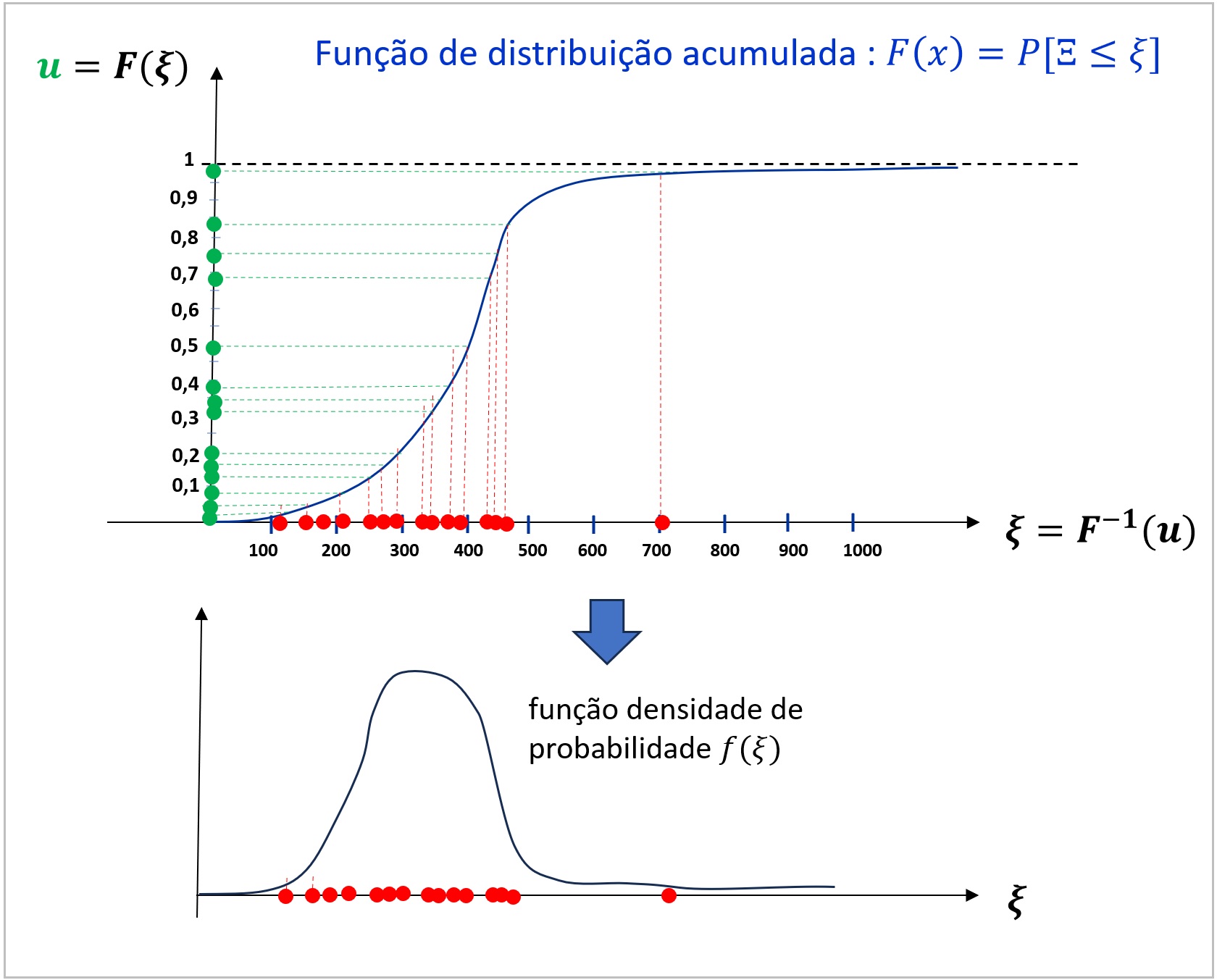
Uma deficiência importante do método de amostragem aleatória simples, quando aplicado para geração de cenários para a resolução de um problema estocástico, é apresentar uma variabildiade potencialmente grande dos cenários com a semente escolhida. Isso acaba resultando na necessidade de se ter uma maior quantidade de cenários para se ter robustez nos resultados. Por esse motivo, o método de AAS não é recomendado para geração dos cenários backward do NEWAVE, ou para construir a árvore de cenários do DECOMP, mas apenas para gerar cenários para a simulação fina do NEWAVE, ou simulações com o modelo SUISHI.

Para esses processo, recomenda-se utilizar métodos que apresentam menor variância, como os mostrados a seguir.

Método k-Means

O algoritmo k-means é uma técnica de clusterização que procura agrupar \(M\) pontos inciais, com dimensão \(n\), em \(K\) objetos, com base nas distãncias entre os pontos. O objetivo é minimizar a soma dos quadrados das distâncias entre os objetos no mesmo grupo. A figura a seguir, extraída do endereço https://medium.com/@englucsantosilva/algoritmo-k-means-na-pr%C3%A1tica-75f4ca656bbc ilustra o algoritmo:

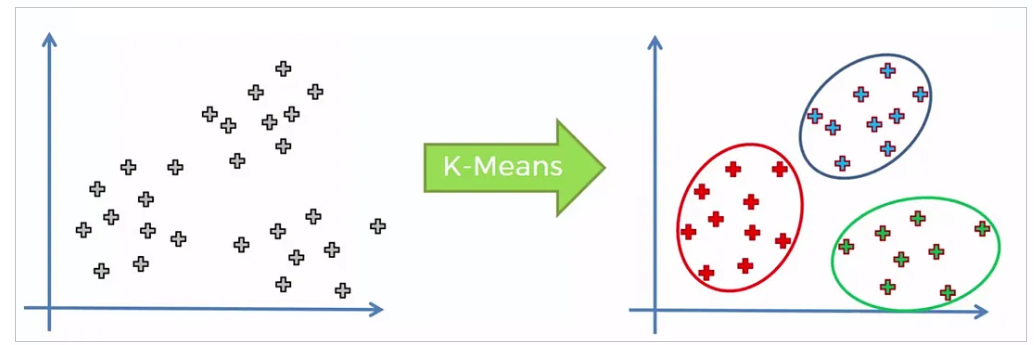
O representante de cada grupo pode ser o centróide ou, caso se deseje utilizar como representante um ponto que foi de fato gerado originalmente, pode-se escolher o ponto mais próximo do centróide. Uma análise comparativa dessas alternativas, mostrando algumas vantagens de se utilizar o centróide é apresentada em 4, 5.

O algoritmo k-means é a base da estratégia de Amostragem Seletiva (AS), que é utilizado pelo modelo GEVAZP na geração dos cenários backward do NEWAVE, assim como na geração de cenários para o modelo DECOMP. A principal vantagem desse método é promover uma grande redução na variabilidade dos resultados do método de amostragem aleatória simples, visto que, como o conjunto de pontos inciais é muito grande, fica-se pouco suscetível a variações no valor da semente.

Quasi Monte-Carlo (QMC)

O método de Quasi Monte-Carlo (QMC) 6 visa suprir uma deficiência dos métodos de amostragem simples, ao utilizar, ao invés de valores sorteados aleatoriamente, pontos escolhidos de forma mais adequada, que resultam em low discrepancy sequences. Em outras palavras, este método reduz a variância do método de Amostragem Aleatória Simples, acelerando sua convergência com o aumento do tamanho da amostra.

Este método foi aplicado ao problema de planejamento hidrotérmico resolvido por PDDE em 7.

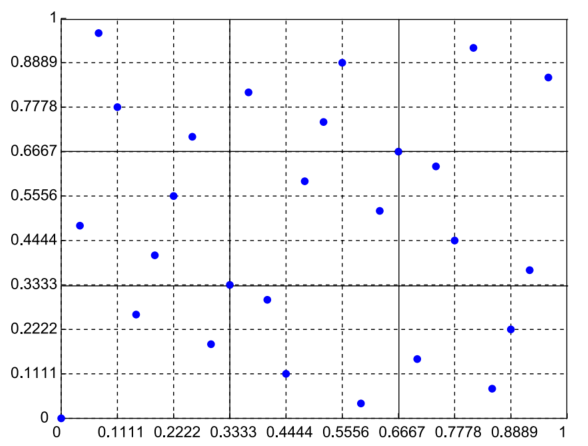
Fonte: 7

Hipercubo Latino (LHS)

É um método de amostragem estratificada, proposto em 8 e cujas boas propriedades para amostras grandes é discutida em 9. Consiste em uma repartição do domínio da variável aleatório em “cubos” com dimensão igual ao da variável, procurando amostrar valores de maneira uniforme ao longo do domínio. Ou seja, procura-se sortear, para cada dimensão da variável aleatória, um valor dentro de cada intervalo ao qual o domínio nesta dimensão é dividido. A combinação entre os valores das diferentes componentes deve ser feita de for a melhor representar a correlação espacial.

Assim, ao mesmo tempo em que se varre de forma mais ampla o domínio da variável, o que pode ser considerada uma limitação do método de Método k-Means (pelo fato de este consierar o centróide de cada grupo), garante-se uma maior estabilidade à variação da semente.

A figura a seguir ilustra o princípio adotado por esse método.

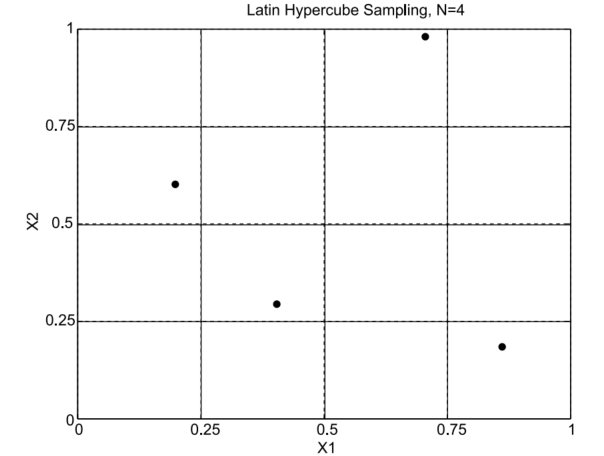
Fonte: 7

A maior dificuldade deste método é garantir uma distribuição adequada desses pontos, para variáveis aleatórias com dimensões muito elevadas.

Aplicações desse método ao problema de planejamento hidrotérmico podem ser encontradas em 7, 10.

Referências

1

Jitka Dupačová, Giorgio Consigli, and Stein W. Wallace. Scenarios for multistage stochastic programs. Annals of Operations Research, 100(1):25–53, 2000. doi:10.1023/A:1019206915174.

2

Hui Li, Zhouyang Ren, Miao Fan, Wenyuan Li, Yan Xu, Yunpeng Jiang, and Weiyi Xia. A review of scenario analysis methods in planning and operation of modern power systems: methodologies, applications, and challenges. Electric Power Systems Research, 205:107722, 2022. doi:https://doi.org/10.1016/j.epsr.2021.107722.

3

Sarjinder Singh. Simple Random Sampling, pages 71–136. Springer Netherlands, Dordrecht, 2003. doi:10.1007/978-94-007-0789-4_2.

4

D. D. J. Penna, F. Treistman, and M. E. P. Maceira. Avaliação de alternativas para escolha do representante no processo de agregação da amostagem seletiva. Relatório Técnico 13612-2018, CEPEL - Centro de Pesquisas de Energia Elétrica, 2018.

5

F. Treistman, L. C. Brandão, D. D. J. Penna, M. E. P. Maceira, and H. S. Araújo. Avaliação do uso do centroide no processo de agregação da amostragem seletiva na geração de cenários de afluências para o planejamento da operação de curto prazo. Relatório Técnico 3383/2019, CEPEL - Centro de Pesquisas de Energia Elétrica, 2019.

6

R. Niederreiter. Random Number Generation and Quasi-Monte Carlo Methods. SIAM, Philadelphia, 1992.

7(1,2,3,4)

T. Homem-de-Mello, V. L. de Matos, and E. C. Finardi. Sampling strategies and stopping criteria for stochastic dual dynamic programming: a case study in long-term hydrothermal scheduling. Energy Systems, 2:1–31, 2011.

8

M. D. Mckay, R. J. Beckman, and W. J. Conover. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics, 21(2):239–245, 1979.

9

Michael Stein. Large sample properties of simulations using latin hypercube sampling. Technometrics, 29(2):143–151, 1987.

10

Xiaolin Ge, Shu Xia, and Wei-Jen Lee. An efficient stochastic algorithm for mid-term scheduling of cascaded hydro systems. Journal of Modern Power Systems and Clean Energy, 7(1):163–173, 2019. doi:10.1007/s40565-018-0412-6.

11

este sorteio pode ser realizado utilizando a função “ALEATORIO()” no Microsoft Excel.