Modelo Autorregressivo Periódico - Par(p)¶
o ajuste do modelo Par(p) para cada uma das usinas principais do Sistema Interligado Nacional (SIN) envolve uma série de passos mostrados na Fig. 2.

Fig. 2 Fluxograma para ajuste do modelo Par(p)¶
A seguir estes passos serão explicados detalhadamente.
Cálculo das Estatísticas Históricas¶
Para a estimação do modelo Par(p) inicialmente definem-se as estatísticas históricas da série temporal.
Para uma série temporal \(Z_t\) podermos estimar os seguintes índices estatísticos:
Média Amostral:
O desvio padrão amostral mede o grau de dispersão da amostra em torno da média:
A assimetria mede o quanto a distribuição de probabilidade de uma variável aleatória se desvia da distribuição normal. Em outras palavras, ela indica se a distribuição é simétrica ou não.
A (4) descreve o cálculo da assimetria utilizando o Coeficiente de Assimetria de Pearson 1. Se o resultado for positivo, indica uma assimetria positiva (cauda direita), enquanto se for negativo, indica uma assimetria negativa (cauda esquerda). Se for zero, a distribuição é simétrica.
Se o resultado for positivo, indica uma assimetria positiva (cauda direita), enquanto se for negativo, indica uma assimetria negativa (cauda esquerda). Se for zero, a distribuição é simétrica.
A covariância mede a extensão da relação linear entre duas variáveis aleatórias separadas por um intervalo de tempo. No contexto hidrológico, a covariância de ordem um expressa a relação linear entre a vazão de um ano e a vazão do ano anterior, conforme indicado pela equação (5):
A covariância tem dimensões proporcionais ao quadrado da variável Z. Para uma avaliação mais direta, normaliza-se a covariância de ordem um pelos desvios padrão das variáveis, resultando na correlação de ordem um, conhecida como dependência serial anual:
Se o valor desta correlação for igual a 1, indica que a vazão de um ano é perfeitamente prevista pela vazão do ano anterior. Um valor de -1 sugere uma correlação perfeita, mas com a inversão da relação entre as variáveis. Um valor próximo de zero indica falta de dependência linear entre as variáveis.
Além disso, é possível medir a dependência espacial entre as vazões afluentes a duas usinas hidroelétricas através da correlação “cruzada” ou correlação espacial entre elas. Por exemplo, a correlação espacial anual entre as vazões afluentes às usinas hidroelétricas A e B é calculada pela seguinte equação:
Em geral, os processos físicos em escala mensal exibem comportamentos periódicos devido aos ciclos sazonais. Cada período possui características estatísticas próprias, como média, desvio padrão e estrutura de correlação sazonal.
A média amostral de cada mês é dada por (8).
De forma análoga o desvio padrão amostral de cada mês é dado por (9).
E a assimetria de cada mês é dada por (10).
Em processos mensais é comum definir um conjunto de valores que descreva a estrutura de correlação linear de um dado mês com os meses anteriores. Esses valores podem ser definidos pela correlação de ordem 1, que descreve a dependência linear da variável aleatória de um mês qualquer \(m\) com a variável aleatória do mês imediatamente anterior \(m-1\); correlação de ordem 2, que descreve a dependência linear da variável aleatória do mês \(m\) com a variável aleatória do mês \(m-2\); …; correlação de ordem \(k\), que descreve a dependência linear da variável aleatória do mês \(m\) com a variável aleatória do mês \(m-k\). A esse conjunto de valores dá-se o nome de função de autocorrelação do mês \(m\), também conhecida por dependência serial mensal.
Os valores amostrais desses índices estatísticos podem ser obtidos pela expressão (11).
Modelo Autorregressivo Periódico - Par(p)¶
Séries hidrológicas têm como característica o comportamento periódico das suas propriedades probabilísticas, como por exemplo a média, a variância, a assimetria e a estrutura de autocorrelação.
Essas séries costumam ser representadas por modelos autorregressivos periódicos, PAR(\(p_m\)), onde \(p_m\) é a ordem do modelo para o período sazonal \(m\), ou seja, é o número de termos autorregressivos do modelo para aquele período.
No caso de séries com sazonalidade mensal temos \(m = 1, ..., 12\) e o modelo PAR(\(p_m\)) pode ser descrito matematicamente pela expressão (12) 2.
Símbolo |
Descrição |
|---|---|
\(t\) |
índice de tempo em função do ano \(i (i = 1, 2, ..., N)\) e do mês \(m\), totalizando T períodos |
\(m\) |
mês |
N |
número de anos |
T |
número total de períodos |
\(Z_t\) |
valor da série no período \(t\) |
\(\mu_m\) |
média de afluência no mês \(m\) |
\(\sigma_m\) |
desvio padrão no mês \(m\) |
\(p_m\) |
ordem do modelo autoregresivo no mês \({m}\) |
\(\phi_{p_m}\) |
operador autoregressivo de ordem \({p_m}\) |
\(a_t\) |
ruído independentes com média zero e variância \({\sigma_{a_m}}^2\) |
A variância do resíduo (\(\sigma_{a_m}^2\)) é dada por (13).
Identificação da Ordem do Modelo¶
A identificação da ordem \(p\), em cada mês \(m\), para o modelo PAR(\(p_m\)) é realizada por meio da análise da função de autocorrelação parcial (PACF). Em um modelo PAR, a PACF possui valor significativo apenas para os primeiros \(p\) lags. Por exemplo, se a PACF mostra uma correlação significativa apenas no lag 1 e não em lags subsequentes, isso sugere que um modelo PAR de ordem 1 pode ser apropriado para modelar a série temporal.
Para determinar a PACF é, necessário estabelecer o número máximo de períodos de dependência. Quando aplicado a um modelo adaptado para a periodicidade mensal das afluências, esse limite máximo corresponde ao número de meses do ano menos 1, ou seja, 11.
Neste caso, obtém-se a autocorrelação (\(\rho_{m}(k)\)) para cada \(k = 1,\dots,11\). Para cada \(k\) verifica-se se o valor da autocorelação é significativo em relação a um intervalo de confiança estabelecido. No modelo PAR(p) do CEPEL é considerado um intervalo de confiança de 95% com um tamanho da amostra igual ao número de anos do histórico de afluências.
Uma vez identificado o maior valor significativo, o respectivo \(p_m\) é atribuído ao modelo e resolve-se as equações de Yule-Walker para a ordem máxima \(p_m\) de forma a definir os coeficientes \(\phi_{k}^{m}, k = 1,\dots,p_m\).
Cálculo dos coeficientes do modelo Par(p)¶
Multiplicando-se ambos os lados da equação do modelo PAR (12) por \((\frac{{z_{i,{m-k}} - \mu_{m-k}}}{{\sigma_{m-k}}})\) e aplicando-se o valor esperado, tem-se a expressão (14).
Substituindo pela expressão de correlação dada por (11) e considerando \(k=1\) a expressão resultante é dada por (15).
Fixando-se \(m\) e variando \(k\) de 1 a \(p_m\) obtemos um conjunto de equações conhecidas como equações de Yule-Walker. Para um mês \(m\) é dada por (16)
Ao se resolver o sistema linear obtém-se os coeficientes lineares do modelo PAR(p) \(\phi_{k}^{m}, k = 1,\dots,p_m\). O sistema linear é resolvido utilizando-se a Decomposição de Cholesky.
Tratamento de coeficientes negativos¶
Um coeficiente autorregressivo negativo pode provocar a presença de um coeficiente positivo no corte de Benders (FCF) associado à variável de estado afluência passada.
Coeficientes positivos nos cortes de Benders têm origem nos coeficientes autorregressivos negativos do modelo estocástico de afluências.
Entretanto, a presença de coeficientes autorregressivos negativos não necessariamente implica coeficientes positivos nos cortes de Benders.
Para lidar com os coeficientes negativos o GEVAZP verifica primeiramente se o coeficiente de ordem 1 de um determinado mês é zero. Se for, o modelo é ajustado a ordem zero.
É preciso então verificar o coeficiente do mês que combina o coeficiente do modelo PAR(p) e modelo PAR(p)-A. Se este coeficiente combinado é menor que zero então reduz-se a ordem do modelo. Esta redução ocorre até que não se encontrem mais coeficientes negativos.
Ao reduzir a ordem do modelo, novos parâmetros devem ser estimados. Este procedimento deve ser repetido até que o conjunto de parâmetros de todos os meses não produza contribuição negativa em qualquer mês futuro.
Cálculo dos Resíduos Históricos¶
Tendo definido a ordem do modelo para o mês \(m\) via PACF e estimados os coeficientes por meio de (16), pode-se calcular os resíduos da série histórica a partir do registro histórico de vazões. Para isso, isola-se o resíduo \(a_t\) na (12), conforme (17).
O cálculo dos resíduos históricos é importante para verificação da qualidade do modelo ajustado. Se o modelo foi ajustado de forma correta os resíduos históricos devem possuir média nula, devem ser independentes e identicamente distribuídos e não apresentarem correlação temporal.
Os resíduos históricos calculados são mostrados no arquivo parp.dat gerado pelo NEWAVE conforme Fig. 3.
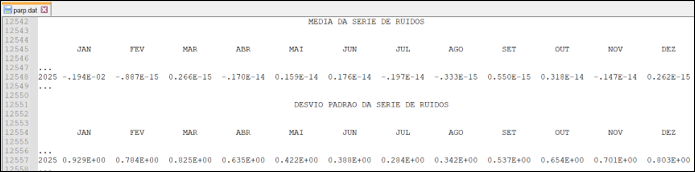
Fig. 3 Resíduos Históricos apresentados no arquivo parp.dat¶