Processo de Modelagem das Incertezas¶
No problema de Planejamento Hidrotermo-eólico considerado nos modelos de otimização energética, o vetor aleatório \(\xi\) possui as seguintes componentes:
\(\xi^t := \{Qinc_1^t,Qinc_2^t,\dots,Qinc_{NH}^t,Vel_1^t,Vel_2^t,\dots,Vel_{NEOL}^t\}\)
onde \(Qinc_i^t\) é a afluência natural a cada uma das \(NH\) usinas hidrelétricas e \(Vel_i^t\) é a velocidade do vento em cada um dos \(NEOL\) parques eólicos, para cada período de tempo.
Portanto, a rigor, será necessário modelar, para cada período \(t\) uma Distribuição de probabilidades conjunta para a variável aleatória multi-variada \(\{\xi_i, i=1,\dots, NH \times NEOL\}\), o que é uma tarefa bastante complexa. Além disso, a existência de dependência temporal faz com que, a rigor, tívessemos que representar a distribuição conjunta não só das variáveis em determinado período \(t\), mas também das variáveis pertencentes a todo o horizonte de estudo.
Entretanto, algumas características das variáveis aleatória e/ou da estratégia de solução permitem que se adote os seguintes procedimentos para a modelagem das variáveis aleatórias:
Como as variáveis aleatórias de diferentes naturezas (ex: afluências às usinas e velocidade de vento) possuem características estatísticas distintas, torna-se interessante utilizar modelos distintos para cada um desses conjuntos de variáveis;
Mesmo dentro de cada conjunto de variáveis aleatórias, torna-se interessante extrair a série temporal referente a cada componente \(i\) do vetor aleatório, que será calibrado separadamente.
Estes dois passos permitem, portanto, que seja feita, em um primeiro momento, uma modelagem individual para cada componente do vetor aleatório, ou seja, cada variável aleatória referente a determinado elemento do sistema (usinas hidrelérica ou parque eólico). Posteriormente, é levada em consideração a correlação espacial entre esses componentes, sejam de um mesmo tipo (correlação entre vazões de diferentes usinas ou ventos de diferentes parques eólicos) ou a correlação espacial entre as vazões afluentes e os ventos. Isto é necessário porque, conforme descrito na seção de Motivação, em, um problema de otimização estocástica, cada cenário de incerteza a ser considerado nos modelos deve conter, de forma conjunta, valores para todos os componentes da variável aleatória.
Ainda que existam particularidades na Modelagem da incerteza hidrológica e Modelagem da incerteza dos Ventos, o processo geral de modelagem das incertezas de uma variável aleatória seguem os passos listados a seguir e descritos na sequência.
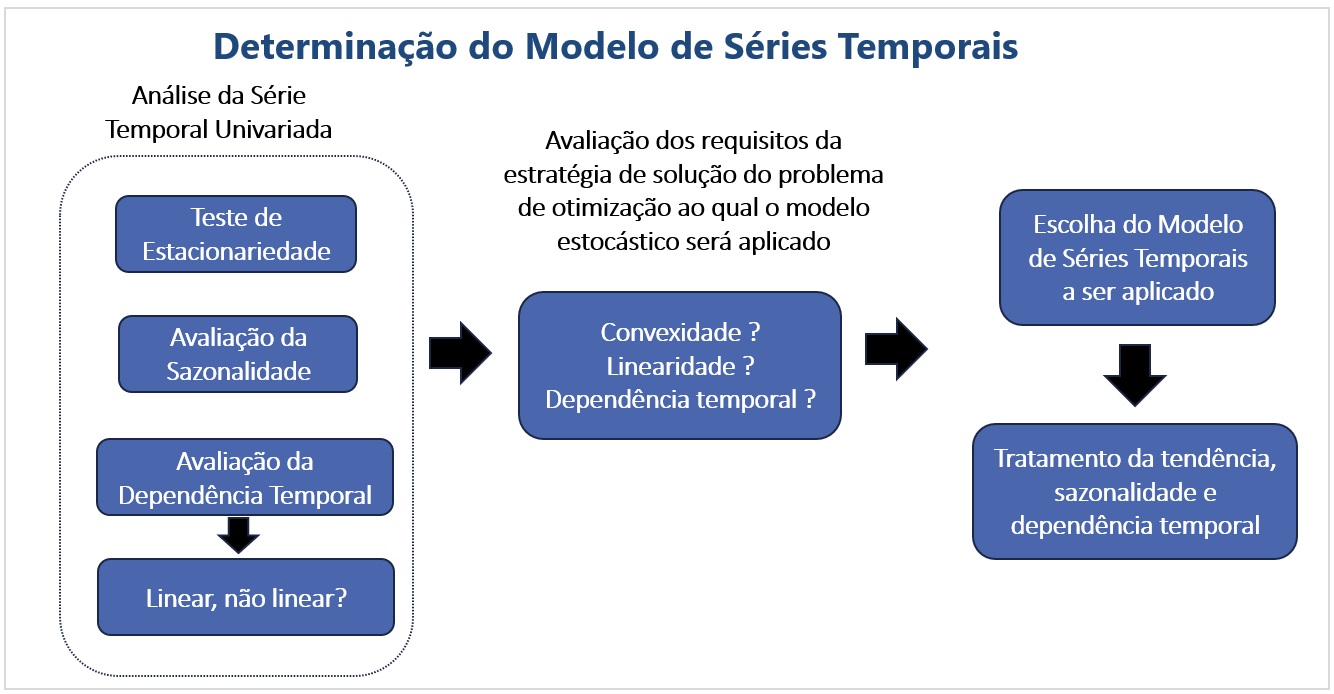
Avaliação do Modelo de Séries Temporais¶
A partir da série histórica individual para cada componente do vetor aleatório (usina hidrelétrica ou parque eólica), procede-se uma avaliação da série temporal, relacionada a esse componente, conforme mostrado a seguir.
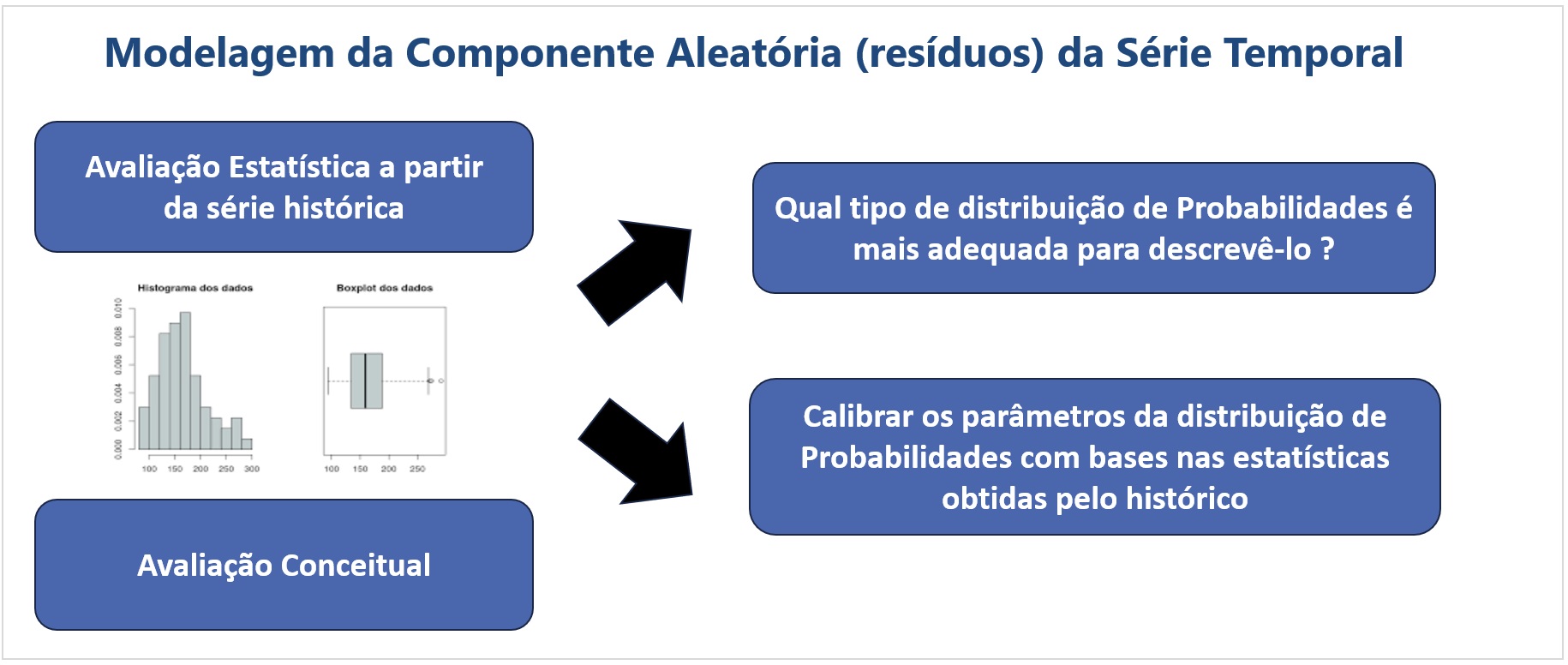
Avaliação da Distribuição dos resíduos¶
Uma vez extraída a sazonalidade, tendência (se for o caso) da série temporal, pode-se obter um processo estocástico estacionário, o qual, após ter sua eventual dependência temporal adequadamente tratada, possui um componente aleatório, que é denominado de resíduo. Este resíduo pode então ser modelado por uma Distribuição de probabilidades, utilizando os passos a seguir.
Tratamento da Correlação Espacial e Temporal¶
Uma vez aplicados os processos descritos nas seções acima, obtêm-se as determinadas as distribuições de probabilidades de cada componente do vetor aleatório, que são denominadas de distribuições de probabilidade marginais. As correlações cruzadas entre as variáveis aleatórias dentro de um mesmo período (correlação espacial) como em períodos distintos (correlação temporal) são tratados, de forma geral, como segue:
as correlações espaciais são introduzidas depois de sorteados o conjunto de resíduos para cada componente da variável aleatória, no processo de Geracao de Cenários;
as dependências temporais são introduzidas na formulaçãço matemática do problema de otimização, utilizando-se os parâmetros obtidos quando da calibração do modelo de série temporal para cada componente. Uma vez que o processo de decomposição temporal do problema faz com que as variáveis aleatórias de períodos diferentes se situam em subproblemas de otimização distintos, as variáveis aleatórias de determinado período \(t\) tornam-se variáveis de estado para os subproblemas dos períodos de tempo subsequentes.