Modelos de Curva de Saturação

As curvas de saturação dos modelos de geradores são definidas a parte, por meio de código próprio (DCST). O Anatem dispõe de quatro tipos de curvas de saturação, selecionadas a partir do preenchimento do campo Tp da régua de entrada de dados, conforme a relação a seguir:

Nc	Número de identificação da curva de saturação a ser utilizada no campo Cs do código DMDG
Tipo	Indica o tipo de equação usada para a curva de saturação
P1	Valor de \(Y_1\) para os tipos 1, 3 e 4 ou valor de \(A\) para o tipo 2
P2	Valor de \(Y_2\) para os tipos 1, 3 e 4 ou valor de \(B\) para o tipo 2
P3	Valor de \(X_1\) para os tipos 1, 3 e 4 ou valor de \(C\) para o tipo 2

Ver também

Veja a entrada Obtenção de Parâmetros da Curva de Saturação para Entrada de Dados no Anatem para mais detalhes acerca da obtenção dos parâmetros a partir de curvas experimentais.

Modelos Exponenciais

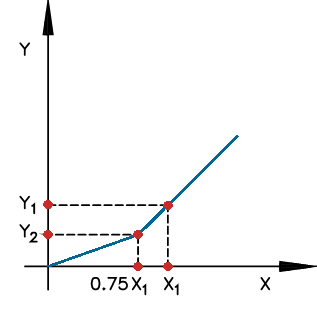
Curva de saturação exponencial com descontinuidade (tipo 1)

Esta curva possui o seguinte equacionamento:

\(x < 0.75 X_1 \Rightarrow y =0\)

\(x \geq 0.75 X_1 \Rightarrow y = Ae^{B(x-C)}\)

sendo:

\(A = Y_2\)

\(B = \frac{\ln\left(\frac{Y_1}{Y_2}\right)}{0.25X_1}\)

\(C = 0.75X_1\)

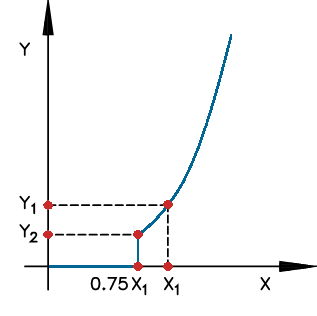
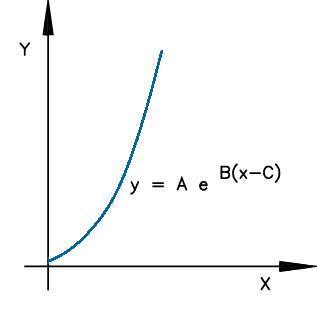
Curva de saturação exponencial (tipo 2)

Esta curva possui o seguinte equacionamento:

\(y = Ae^{B(x-C)}\)

Modelos Lineares

Curva de saturação linear (tipo 3)

Esta curva possui o seguinte equacionamento:

\(x < C \Rightarrow y =0\)

\(x \geq C \Rightarrow y = Ax+B\)

sendo:

\(A = \frac{Y_1-Y_2}{0.25X_1}\)

\(B = Y_1 - A X_1\)

\(C = -\frac{B}{A}\)

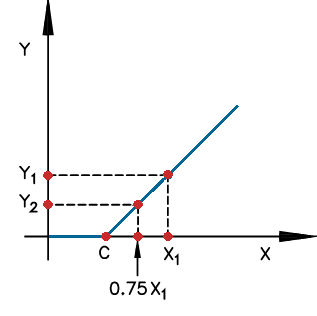
Curva de saturação linear por partes (tipo 4)

Esta curva possui o seguinte equacionamento:

\(x < 0.75 X_1 \Rightarrow y = Cx\)

\(x \geq 0.75X_1 \Rightarrow y = Ax+B\)

sendo:

\(A = \frac{Y_1-Y_2}{0.25X_1}\)

\(B = Y_1 - A X_1\)

\(C = -\frac{Y_2}{0.75 X_1}\)