Bloco FUNCAO Subtipo PONTOS¶
O subtipo PONTOS do bloco FUNCAO permite interpolar uma curva a partir de um conjunto de pontos definidos. O valor de saída do bloco é lido sobre a curva construída partir do valor de entrada. É necessário definir ao menos três pontos para a curva, sendo necessariamente \(X_{i+1} > X_i\) e \(Y_{i+1} \neq Y_i\).
Características¶
# Entradas |
1 |
Sinal de Entrada |
Real |
Sinal de Saída |
Real |
P1 |
Coordenada \(X\) para o i-ésimo ponto; obrigatório |
P2 |
Coordenada \(Y\) para o i-ésimo ponto; obrigatório |
P3 |
Coordenada \(X\) para o i+1-ésimo ponto |
P4 |
Coordenada \(Y\) para o i+1-ésimo ponto |
Valores default |
|
Restrições |
Requer o preenchimento de pelo menos 3 pares (X,Y). \(X_{i+1} > X_i\) e \(Y_{i+1} \ne Y_i\) |
Nota
É possível utilizar os campos P1 e P2 e/ou, analogamente, os pontos P3 e P4 para a definição dos pontos a partir dos quais serão interpolados a curva.

Aviso
O Bloco FUNCAO Subtipo PONTOS é um subtipo de bloco do tipo função. Portanto, para utilizá-lo, é necessário preencher o campo tipo como FUNCAO e o campo stip como PONTOS.
Lógica¶
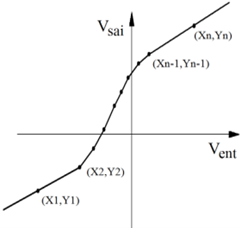
Se \(X_i \leq V_{ent} < X_{i+1}\), para \(i = 1,n-1\), então \(V_{sai} = Y_i + \frac{Y_{i+1} - Y_i}{X_{i+1} - X_i} (V_{ent} - X_i)\)
Se \(V_{ent} < X_1\), então \(V_{sai} = Y_1 + \frac{Y_2 - Y_1}{X_2 - X_1} (V_{ent} - X_1)\)
Se \(V_{ent} \geq X_n\), então \(V_{sai} = Y_{n-1} + \frac{Y_n - Y_{n-1}}{X_n - X_{n-1}} (V_{ent} - X_{n-1})\)
Exemplo¶
1DCDU
2(ncdu) ( nome cdu )
3 01 CDU_PONTOS
4(nb)i(tipo)o(stip)s(vent) (vsai) ( p1 )( p2 )( p3 )( p4 ) (vmin) (vmax)
5 50 FUNCAO PONTOS Vent Vsai 0.00 -.80 0.10 -.778
6 0.25 -.745 0.35 -.723
7 0.40 -.712 0.45 -.701
8 0.50 -.690 0.55 -.679
9 0.60 -.668 0.65 -.657
10 0.70 -.646 0.80 -.624
11 0.90 -.602 1.00 -.580
12 1.10 -.579 1.20 -.578
13FIMCDU
14(
15999999