Funções de Transferência de Segunda ou Terceira Ordem

Este caso exemplo ilustra o comportamento dinâmico do bloco POL(S), utilizado para a representação de blocos dinâmicos de segunda ou terceira ordem.

Dica

A função de transferência do bloco POL(S) é descrita por:

\(\dfrac{P_1^1 s^3 + P_2^1 s^2 + P_3^1 s + P_4^1}{P_1^2 s^3 + P_2^2 s^2 + P_3^2 s + P_4^2} \longrightarrow \frac{P_i^1 = \text{ parâmetros descritos na primeira linha}}{P_i^2 = \text{ parâmetros descritos na segunda linha}}\)

Na definição deste bloco, o denominador deve ter ordem \(\geq 2\) e deve ser obrigatoriamente maior ou igual que a ordem do numerador. Ao menos um dos termos independentes (\(P_4\)) deve ser não nulo.

Nota

Neste caso exemplo será comparada a representação de uma mesma função de transferência de segunda ordem modelada por meio de blocos de primeira ordem e utilizando o bloco POL(S).

O CDU ilustrado na Fig. 97 permite avaliar a resposta de funções de transferência de segunda ordem ao degrau com amplitude \(V\).

(*) Clique na imagem para visualizar os detalhes da figura

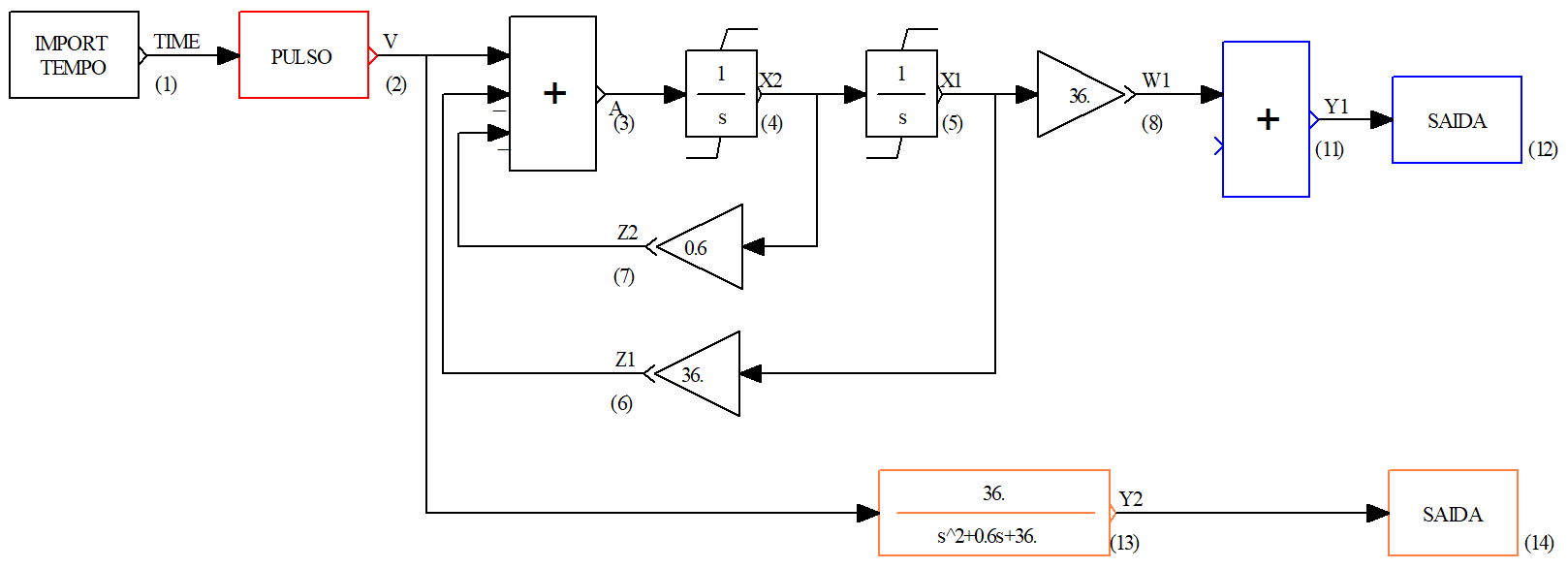
Fig. 97 Caso exemplo com blocos de primeira ordem

Os resultados desta simulação são apresentados na Fig. 98:

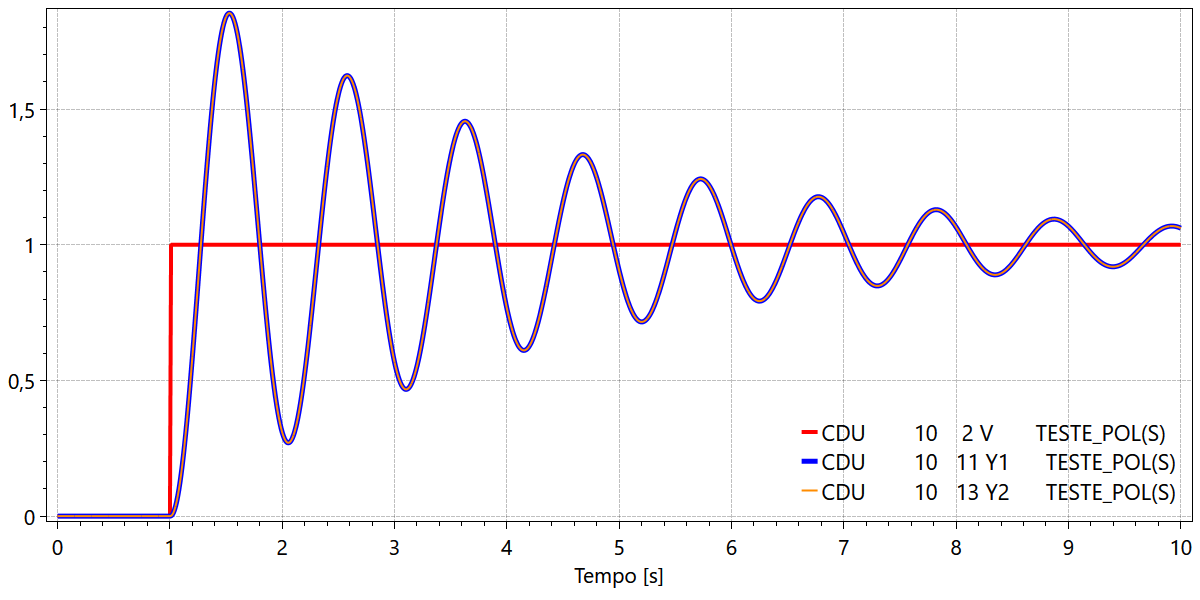
Fig. 98 Resposta ao degrau de blocos de primeira ordem

Nota

Observe que a saída do bloco POL(S) (variável \(Y_2\)) é idêntica a resposta obtida com utilização dos blocos de primeira ordem (variável \(Y_1\)).