Solução de Problemas de Convergência e de Desempenho¶
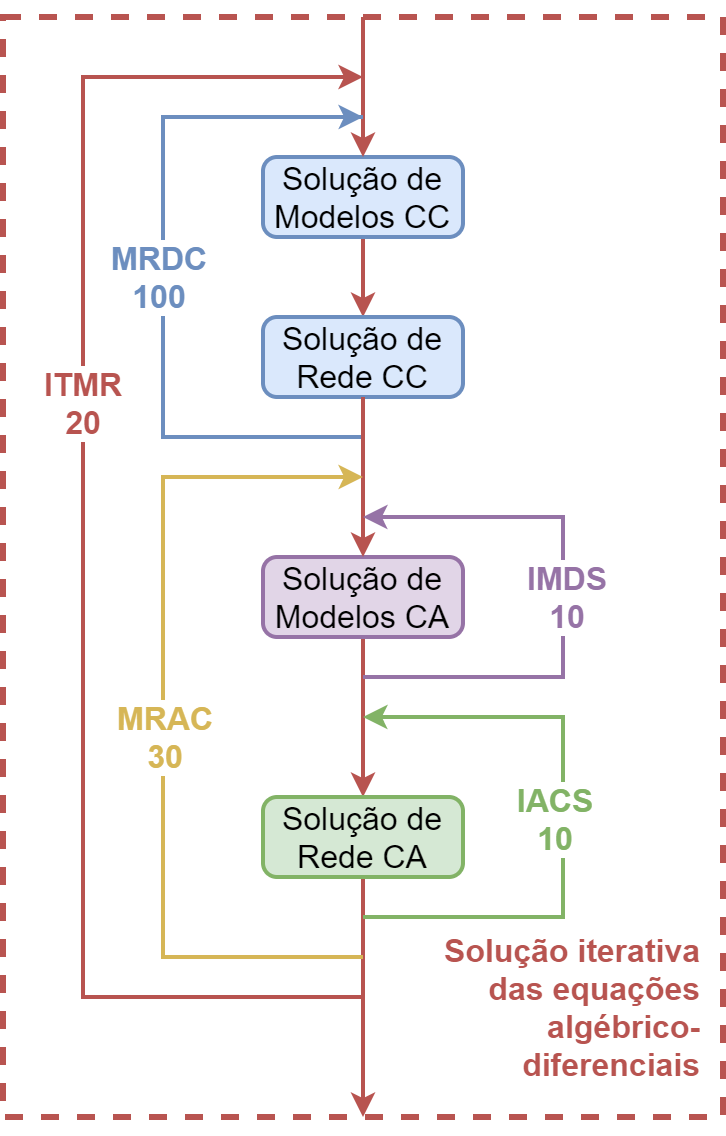
O processo de solução utilizado no programa Anatem consiste em uma solução alternada entre os sistemas CC e CA, onde cada sistema terá inicialmente a solução dos modelos e em seguida da rede, conforme ilustrado na figura abaixo. Nas soluções de rede CA ou CC, a rede elétrica é representada pela matriz de admitâncias nodais e os elementos conectados à rede são representados por injeções de corrente.
O método de solução alternada dos sistemas CA e CC utilizado no Anatem proporciona precisão, robustez e principalmente uma grande eficiência computacional, tanto em relação à economia de memória como em relação a esforço computacional. O método de solução simultânea, baseado na aplicação do método de Newton-Raphson para todas as equações do sistema, por outro lado, embora apresente taxa de convergência quadrática próxima à solução e uma maior robustez quando próximo à solução, apresenta algumas características inferiores ao método alternado como a maior demanda de memória, maior esforço computacional e menor robustez de convergência quando distante da solução ou com chaveamentos em malhas de controle de modelos definidos pelo usuário.
Mesmo com ótimas características, o método de solução alternada pode apresentar problemas de não convergência durante a solução dos subsistemas de maneira não simultânea. Estes problemas podem ser decorrentes de diversos motivos, mas que, de forma geral, podem ser resolvidos, desde que sejam corretamente diagnosticados.
Antes de mais nada….¶
Na maioria dos casos, problemas de desempenho e de convergência podem ser solucionados com ajustes simples que pouco impactam na qualidade da resposta, ou pouco interferem no algoritmo de solução. Inicialmente, atente para os seguintes detalhes:
Passos de integração apropriados: boa parte dos problemas de convergência são resolvidos com a utilização de passos de integração apropriados ao escopo da análise. Para sistemas de grande porte, com muitos equipamentos modelados, recomenda-se a utilização do passo de 1ms para simulações em geral. No caso de eventos próximos a transmissão de corrente contínua, esse passo de integração pode ser reduzido a 0.1ms, enquanto durar os eventos. Para os trechos finais da simulação (geralmente após pelo menos 5 segundos do último evento na rede), passos de 3ms apresentam resultados satisfatórios.
Modelagem incompleta de fontes de geração: em cenários com alta penetração de energia eólica e solar, os modelos dinâmicos dessas fontes devem estar devidamente representados no caso. É possível que a sua representação como modelo ZIP (via código DGER) contribua para os problemas de convergência possíveis de serem observados.
Modelagem inapropriada da carga: o modelo de carga a ser utilizado é um problema a parte que deve ser verificado com toda atenção. Frequentemente, o modelo para transitórios eletromecânicos de uma carga não é equivalente ao modelo estático utilizado nas análises de fluxo de potência. O modelo de Potência Constante, muito utilizado em modelos de fluxo de potência, não é apropriado para estudos de transitórios eletromecânicos, por exemplo. Idealmente, esses modelos devem ser levantados a partir da observação experimental da carga em função das condições operativas do sistema.
Parâmetro Vmin do modelo de carga: Alteração do parâmetro original para um valor maior (ex. 0.8 pu) para conversão da carga em Z constante quando a tensão passa a ser muito baixa, evitando erros de convergência da rede CA. Esta não convergência da rede CA é indicada como erro no arquivo de saída (OUT). Isto ocorre pois a rede CA em colapso ou em defeito pode não ter capacidade de atendimento à carga e isto está associado a uma não solução matemática da rede CA (potência das cargas acima da margem de estabilidade de tensão do sistema).
Acerto nas constantes de convergência: o Anatem utiliza como padrão constantes de convergência que se mostraram robustas ao longo de anos de estudos de transitórios eletromecânicos. Em alguns casos específicos, contudo, essas constantes podem ser alteradas para possibilitar a simulação de casos excepcionais, quando nenhuma outra alternativa tentada logrou resultado. Muitas vezes, essas alterações de constantes são carregadas nos arquivos de estabilidade do Anatem. Verifique se existem dados personalizados de constantes de convergência no caso: frequentemente essas mudanças mais prejudicam que ajudam.
Separação de eventos em instantes (passos de integração) distintos: ao invés de aplicação de múltiplos eventos de forma simultânea, recomenda-se realizar a aplicação de defeitos em etapas.
Dados de falha de comutação por nível de tensão: recomenda-se utilizar valores da ordem de 0.7 pu. Em redes com defeito, pode não haver solução matemática para a injeção transitória do elo, durante este período e, na prática, quando isto ocorresse provavelmente haveria a falha de comutação dos inversores. A não utilização deste critério pode levar à não convergência da rede CA. Normalmente esses dados já são fornecidos nos bancos de dados dinâmicos. Verifique se não estão comentados (removidos da simulação) indevidamente.
Problemas nos dados de rede elétrica¶
Alguns dos problemas de convergência são decorrentes das características da rede CA. Em geral, não é esperado que o usuário precise alterar dados da rede elétrica, a menos daqueles relativos ao objeto de estudo.
O problema do mal condicionamento é independente do modelo de carga e geração; a diferença é que modelos funcionais ou dinâmicos antecipam a ocorrência. Ao longo do processo iterativo, o erro numérico é acumulado em função da alta sensibilidade da solução do sistema linear e, eventualmente, essas barras escapam da região de convergência e demoram muitas iterações para retornarem.
O problema de convergência devido aos dados da rede elétrica podem ser observados por dois fatores:
A simulação apresenta bom desempenho computacional, até que, a partir de determinado ponto arbitrário, o desempenho computacional fica severamente prejudicado, independente de qualquer evento ou ocorrência.
O relatório de convergência RCVT aponta para uma rede CA que inicializa o processo iterativo com um mismatch baixo (em geral de \(10^{-4}\) a \(10^{-5}\)), mas necessita de 10 ou mais iterações para convergir. Para um mismatch nessa ordem de grandeza, o esperado era a convergência em uma ou duas iterações.
Desta forma, é importante ficar atento para os seguintes pontos:
Relação X/R dos circuitos: redes de transmissão possuem a relação X/R elevada, muitas vezes a resistência do circuito é até desprezada. Em função dessa característica, os métodos numéricos utilizados para a solução do fluxo de potência fazem uso dessa característica para garantir a convergência com menos empenho computacional. É recomendado que, na modelagem da rede de distribuição para acoplamento a uma rede de transmissão, a relação X/R não deverá ser menor do que 10, mesmo que isso não seja a representação original da rede de distribuição. Note que, neste caso, a representação da rede de distribuição é simplificada.
Baixo valor para impedância de circuitos radiais: a baixa impedância resulta numa alta sensibilidade da solução numérica (mal condicionamento do sistema linear), tornando o processo iterativo com convergência sublinear, em comparação à convergência quadrática esperada. Não utilize reatâncias inferiores a 0.01% em sistemas radiais e, preferencialmente, utilize valores superiores a 0.1% para reatância.
Problemas na modelagem de controladores CDU¶
Alguns dos problemas de convergência podem decorrer da modelagem inapropriada de controladores CDU. Estes problemas podem se manifestar de algumas formas:
Controles individualmente problemáticos: em alguns casos, alguns controles, em si, apresentam problemas internos de convergência. Este fenômeno é geralmente evidenciado pelo uso da opção ESTC (estatística de convergência de CDUs) junto ao código EXSI (piores casos) ou ao código RELA (completo). Nesta situação, alguns controladores aparecerão no topo da lista com valores de convergência sensivelmente superiores aos demais, destacando-se. O índice de severidade, medido como a quantidade de desvios-padrões da média, também é um indicativo do quão complicado são aqueles controles dentro do conjunto de CDUs simulados.
O principal motivo pelo qual um CDU pode apresentar um problema de convergência interno está nos laços de realimentação com termos de transmissão direta. Isto significa, que em alguma medida, uma malha de controle apresenta entrada \(x(t)\) e saída \(y(x(t))\), sendo que a sua entrada também acaba sendo uma função do valor da saída, ou \(x(y(t))\). Quando a realimentação promove um ganho (em transmissão direta) menor do que 1, qualquer \(\Delta y_k\) encontrado na solução representará um \(\Delta x_{k+1} < \Delta y_k\), que por sua vez implicará em uma reavaliação do novo valor da saída cuja variação deverá ser inferior ao \(\Delta y_{k+1}\) da iteração anterior (teorema dos pequenos ganhos).
Quando a condição anterior é observada, o sistema apresenta convergência em potencial. Contudo, em algumas realimentações, especialmente verificado em lógicas de proteção, verifica-se o uso de blocos lógicos que apresentam realimentação direta, sem atrasos (DELAY). Como a saída dessas malhas é sempre 1 ou 0, a hipótese do teorema dos pequenos ganhos não é verificada e a convergência numérica não é garantida.
Em algumas malhas com variáveis contínuas, o fenômeno também pode ocorrer. Em particular, frequentemente limites de alguma variável são função da própria variável de saída. Neste sentido, quando o limite cresce no mesmo sentido que a variável, existe uma realimentação negativa que pode ocasionar num problema de não-convergência. A recomendação, nestes casos, estaria em usar um bloco de atraso (DELAY) para remover a sensibilidade instantânea do limite.
O modelador deverá ter cuidado, portanto, ao realimentar malhas em laços onde existe termo de transmissão direta. O princípio do teorema dos pequenos ganhos, onde a realimentação precisa provocar ganhos decrescentes no processo iterativo, deve ser observado para uma garantia de solução no processo de convergência.
Controles em conflito com a rede: outra possibilidade reside em modelos cuja convergência interna é rápida, mas sua saída é extremamente sensível a variáveis de entrada do problema. Geralmente isso decorre de não-linearidades que apresentam descontinuidades (intencionais ou acidentais), onde pequenas variações internas no modelo poderiam causar variações bruscas nas variáveis de saída, aumentando o erro dentro do processo de convergência. A detecção deste problema difere do anterior: neste caso, este problema se evidencia por meio de uma elevada taxa de iteração entre modelo-rede. Individualmente, o controle pode não prevalecer sobre os demais; contudo, ao analisar o relatório de convergência RCVT, será possível observar que o programa, quando alterna entre a solução do modelo para a rede, encontra um erro relativo alto, conforme o exemplo a seguir:
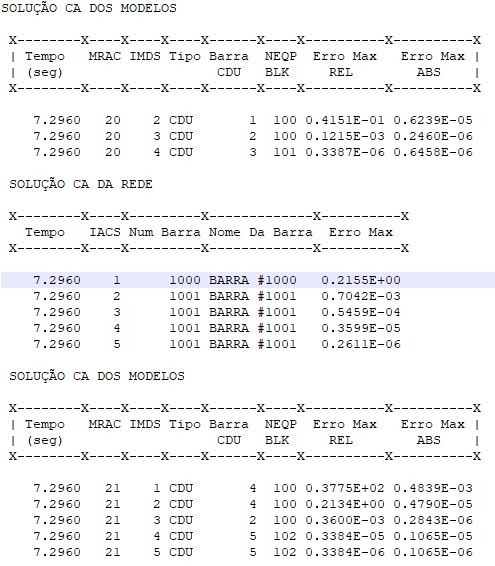
Fig. 106 Exemplo ilustrativo de um problema ocasionado por um controlador conectado a barra #1000. O controlador problemático em si não aparece na relação anterior.¶
No caso anterior, a barra #1000 apresenta problemas de convergência em função de um controlador conectado a um equipamento nesta barra, embora o controlador em si não figurasse na relação dos controladores com problema de convergência.
Problemas na importação do ângulo da barra: outra possibilidade de erro de modelagem consiste na importação do ângulo da barra. No Anatem, o ângulo de uma barra é calculado em função da distância angular entre aquela barra e o centro de massa elétrico. Isto significa que, na ocorrência de uma descontinuidade do conjunto que forma o centro de massa elétrico (como o ilhamento), o ângulo variará instantaneamente. Malhas de controle que sejam sensíveis a frequência do sistema, e estejam usando essa variável de ângulo para estimar a frequência, avaliarão incorretamente o salto vetorial como sendo função de uma frequência elevada, o que não é verdade, incorrendo em uma resposta errada pelo controlador.
Além disso, a variável de ângulo é determinada pela abertura angular entre as componentes reais e imaginárias da tensão do barramento. Isto significa que a variável é limitada pela relação trigonométrica do arco-tangente da tensão. Assim, sinais de ângulo que estejam abrindo continuamente apresentarão descontinuidade para seu valor mínimo quando cruzarem o limite do domínio desta variável. Este salto no valor do ângulo implica nas mesmas consequências matemáticas descritas no problema anterior.
É possível de se implementar corretamente a evolução do ângulo da barra por meio da lei dos cossenos. O Anatem, contudo, dispõe do Bloco PHASE para levar em consideração essas descontinuidades, apresentando um sinal de saída contínuo. Verifique a documentação do bloco para maiores informações.
Opções para Resolver o Problema de Convergência¶
Caso as observações anteriores não tenham sido suficientes para resolver os problemas de convergência, existem outras alternativas visando alteração no processo de solução iterativo por meio de algumas Opções de Execução (associadas ao código EXSI).
As seguintes Opções de Execução podem ser utilizadas (inclusive simultaneamente), seguindo a seguinte ordem de inserção recomendada:
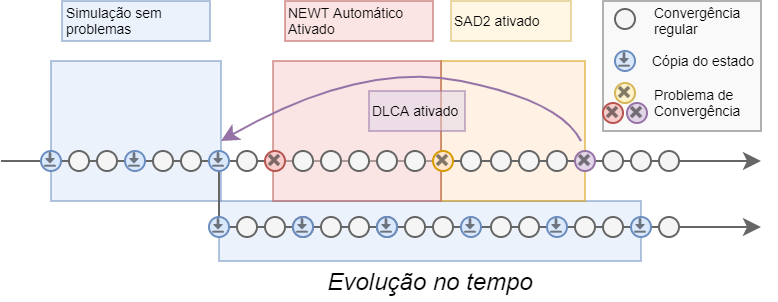
DLCA: adiciona um DELAY na saída de blocos de CDU com problemas de convergência. Pode ser utilizada quando existe um problema na solução de controladores de modelos CA. Não possui efeito sobre a simulação caso não existam problemas de convergência de blocos de CDU. Utilize o Arquivo de Cache do recurso DLCA para uma simulação com melhor desempenho.
SAD2: desacopla a solução CC da solução CA nos momentos em que se detecta um problema de convergência, por TSAD segundos segundos de simulação (tipicamente 10 ms). Pode ser utilizada quando existe um problema na solução dos laços iterativos CA-CC. Não possui efeito sobre a simulação caso não existam problemas na solução do laço CA-CC.
DLCC: desacopla os processos iterativos modelo CC e rede CC, pela inclusão de um atraso de um passo de integração no ângulo de disparo do controle a ser utilizado pelos conversores para solução da rede CC. Esta opção pode ser utilizada quando o pequeno erro entre o modelo CC e rede CC não permite a convergência conjunta entre os processos iterativos. Na utilização da opção DLCC é recomendável utilizar passos de integração reduzidos (0.2 ou 0.1 ms) para que a influência do atraso na dinâmica dos elos de corrente contínua seja desprezível. Deve-se também utilizar esta opção apenas em um curto período de tempo em que haja a necessidade, para evitar a utilização de passo de integração reduzido em toda a simulação.
FLXT: durante a comutação para o método de Newton automaticamente, as tolerâncias de convergência do programa são flexibilizadas. As tolerâncias originais definidas pelo usuário são retornadas assim que o período de simulação do método de Newton automático terminar. É preferível que o usuário utilize essa opção a alterar manualmente as opções de simulação.
CILH: permite a solução da rede CA na ocorrência de ilhamento, sem máquina síncrona de referência. Tradicionalmente, uma ilha elétrica sem referência é considerado um problema de mau-condicionamento. Esta opção tem efeito semelhante à adição de uma referência para terra por meio da adição de um shunt ao caso.
ILHA: realiza o desligamento da ilha elétrica sem referência. É possível que, numericamente, o problema matemático não apresente solução mesmo com adição de uma referência para a terra, em função das injeções passivas do sistema. Caso a opção CILH não tenha resolvido o problema, utilize esta opção para desligar, até o final da simulação, a ilha elétrica.
NEWT: tradicionalmente, o Anatem utiliza o método da injeção de corrente para resolução da rede CA. Em alguns casos, esse método pode apresentar problemas no processo de convergência, e nestes casos o método de Newton aumenta a convergibilidade do caso, em detrimento do desempenho computacional. Não é necessário a aplicação explicita desse método, o Anatem automaticamente habilita esse método quando é verificado um insucesso do processo de convergência. Esse método permanece ativo por aproximadamente 100ms de simulação.
SADD: desacopla a solução CC da solução CA. Pode ser utilizada quando existe um problema na solução dos laços iterativos CA-CC. Utilize a opção SAD2 preferencialmente. Caso usada, essa opção deve ser usada com parcimônia, em trechos pequenos de simulação onde é verificado o problema de convergência.
A figura a seguir ilustra a lógica de atuação do DLCA em conjunto com o SAD2 em um caso problemático:
Opções para Melhoria de Desempenho¶
Outras Opções de Execução que podem ser utilizadas referentes ao desempenho computacional:
DNWT: solução pelo método de Newton-Raphson “desonesto” (Dishonest Newton). É o método de Newton onde o Jacobiano é apenas atualizado na primeira iteração da solução de rede CA, no início do passo. Há ainda a alternativa de atualização de jacobiano com frequência especificada no código DSIM. A opção DNWT, principalmente com a utilização de atualizações menos frequentes, pode ser mais eficiente computacionalmente que o método convencional e certamente é mais eficiente que o método de Newton, embora necessite de mais iterações para alcançar a convergência. Caso existam problemas de convergência, o programa altera o método de solução para o método de Newton (NEWT) automaticamente.
ANWT: solução pelo método de Newton-Raphson adaptativo (Adaptative Newton). É o método de Newton onde o Jacobiano é apenas atualizado quando a taxa de convergência da solução de rede CA é lenta (mais do que cinco iterações). É computacionalmente mais eficiente que o método DNWT, apesar de necessitar de mais iterações para alcançar a convergência. Pode ser mais eficiente que o método convencional do Anatem em alguns casos em que o número de soluções de rede CA seja elevado. Caso existam problemas de convergência, o programa altera o método de solução para o método de Newton (NEWT) automaticamente.
OTMX: a flexibilidade proporcionada pelos CDUs também permite que controladores sejam modelados de forma não ótima. Em muitos casos, malhas de controle são modeladas, apesar de não serem utilizadas pelo controlador (geralmente, malhas de controle alternativas desativadas por algum parâmetro). Esta ativa um recurso do programa em varrer os CDUs definidos e elimina da simulação aqueles blocos que não são capazes de alterar a resposta dinâmica do controle.
Caso / Modo
Sem OTMX
Com OTMX
A
06:36.13
06:30.13
B
17:36.53
15:34.92
SAD3: desacopla a solução CC da solução CA normalmente, realizando um laço de acoplamento entre essas scoluções a cada TSAD segundos segundos de simulação (tipicamente 10 ms). Esta opção traz ganhos quando o número de iterações CA-CC é muito alto.
Caso / Modo
Sem SAD3
Com SAD3
A
04:59.80
03:24.65
B
20:20.54
07:16.29
FLX2: permite que as tolerâncias de convergência TETE, TEMD e TABS sejam flexibilizadas durante a simulação a cada FFLX passos de simulação, realizando um passo de simulação com as tolerâncias originais a cada ciclo. Com essa opção, as constantes passam a assumir valores dez vezes o superior àquelas definidas anteriormente. Esta opção permite que o Anatem consiga realizar mais rapidamente a simulação, com um pequeno erro controlado inserido na simulação.
SPMD: permite a resolução em paralelo dos modelos CA e dos modelos CC. Em geral, é desaconselhável o uso explicito dessa opção. Utilize o atalho F5 da interface gráfica para executar a simulação com paralelismo ligado, ou então o argumento -n X no modo shell.
Caso / Modo
Sem SPMD
Com SPMD
A
04:12.95
02:17.00
B
07:29.86
03:23.42
Código CCDU: alguns modelos de eólica e fotovoltaicas apresentação modelagem de um parque em duas estruturas diferentes (DFNT e DCNE). Em função da ordem de solução dos modelos Anatem, é possível que a ordenação dos modelos não seja ótima para o processo de convergência. Utilize este código para alterar a ordem de solução de modelos onde exista comunicação direta entre modelos DCNE e DFNT, colocando os modelos de DCNE para serem resolvidos antes.
Caso / Modo
Sem CCDU
Com CCDU
A
13:08.44
07:29.84
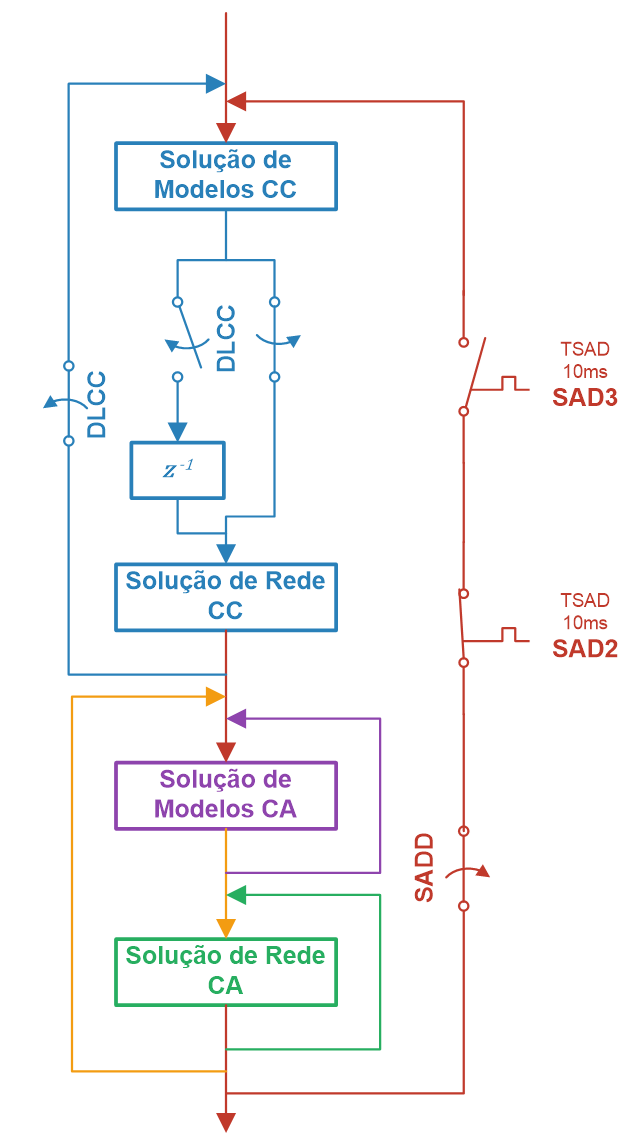
A Fig. 110 ilustra a atuação das opções DLCC, SADD, SAD2 e SAD3 sobre o processo de solução.
Exemplo de Trechos de Simulação Recomendados¶
Abaixo são dados os parâmetros recomendados para simulações com eventos provocados ocorrendo em até 0,2 s envolvendo elos de corrente contínua. Neste conjunto foi utilizado um passo razoavelmente reduzido para o início em conjunto com as opções SAD2 e DLCC, trazendo grande robustez ao processo de solução sem perda de precisão.
1DSIM
2( Tmax ) (Stp) ( P ) ( I ) ( F )
30.19 .001 1 11
4(
5EXSI DLCA OTMX
6(
7DSIM
8( Tmax ) (Stp) ( P ) ( I )
9 0.50 .0001 25
10(
11EXSI DLCC DLCA SAD2
12(
13DSIM
14( Tmax ) (Stp) ( P ) ( I )
15 1. .0005 5
16(
17EXSI DLCC DLCA SAD2
18(
19DSIM
20( Tmax ) (Stp) ( P ) ( I )
21 1. .001 5
22(
23EXSI DLCA
No caso de eventos provocados ocorrendo em pontos com certa distância dos elos de corrente contínua, pode-se utilizar valores menos rígidos, como por exemplo:
1DSIM
2( Tmax ) (Stp) ( P ) ( I )
3
4 0.19 .001 1 11
5(
6EXSI DLCA SAD2 OTMX
7(
8DSIM
9( Tmax ) (Stp) ( P ) ( I )
10 0.50 .0001 25
11(
12EXSI DLCC DLCA SAD2
13(
14DSIM
15( Tmax ) (Stp) ( P ) ( I )
16 1. .001 5
17(
18EXSI SAD2
Recomenda-se fazer uma avaliação prévia de uma simulação com os parâmetros mais rígidos do primeiro conjunto e, caso a resposta seja equivalente ao do segundo conjunto, pode-se utilizar este último para as simulações de todas as contingências na região de interesse do teste.